浙江省第二届高中数学说题比赛题目及解答VIP免费

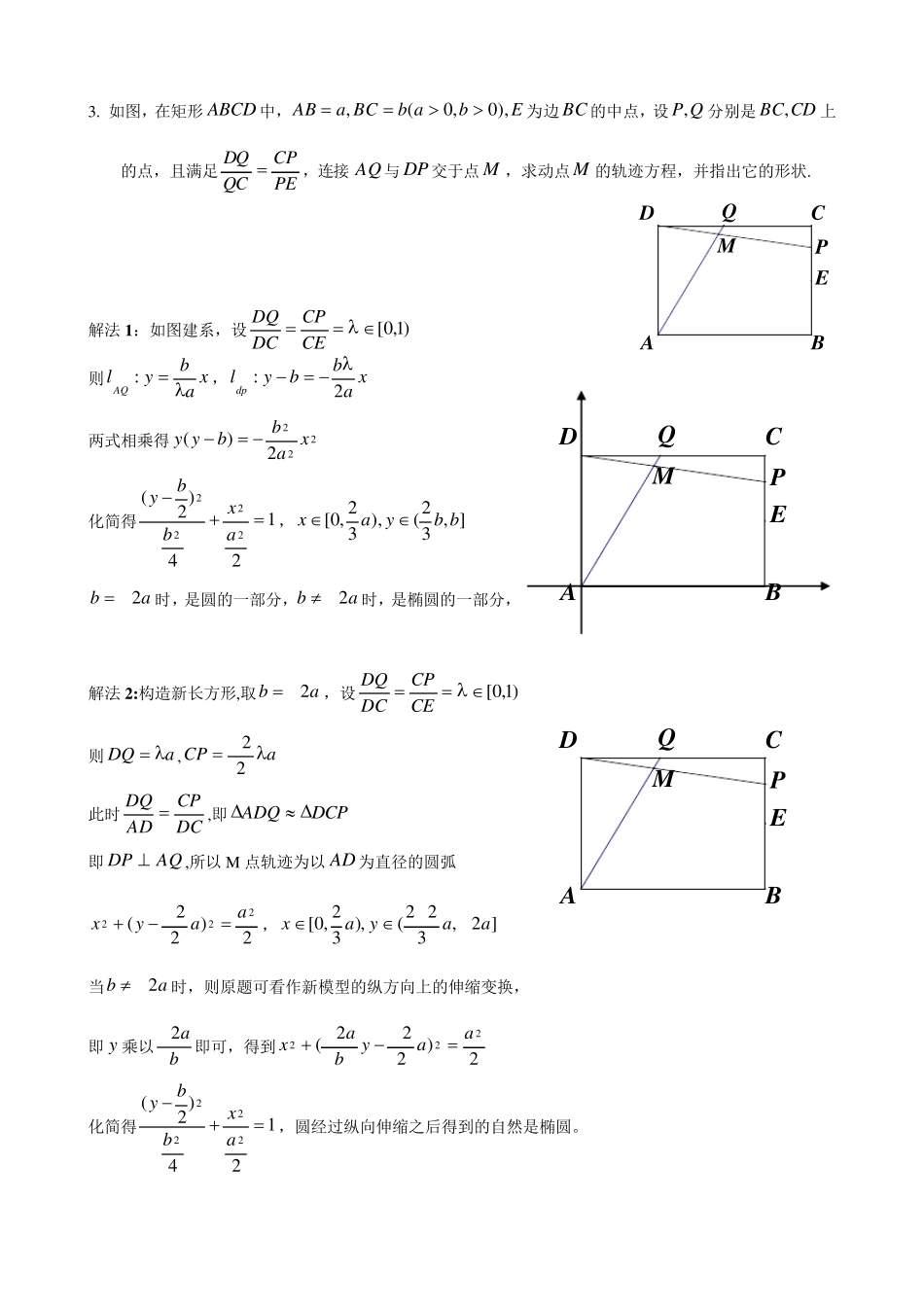
个人赛： 1. 设集合1|),{(abaM，且}mb ，其中Rm.若任意 Mba),(，均有032abab，求实数m 的最大值. 解法1 ：（纯代数解法） 由题意得：0)32(bab对于 1a恒成立.（这里看做a 的一次函数） 于是有0)32()1(032bbb，)32(32bbb（*） 构造函数xxgx  2)(，显然)(xg在R 上单调递增，（*）式转化为)1()(gbg， 也就是1b恒成立， 所以1m，即实数m 的最大值为1. 解法2 ：（数形结合） 由题意得：bab)32(，abb32对于 1a恒成立.（再把b 看做x） 这里32 xy是不变的，而axy是一条绕着原点旋转的直线，其斜率范围是)0,1[1a，要使得axx 32在 ),(m上恒成立，也就是在 ),(m上无论斜率怎样变化，都要满足直线在曲线上方，那么直线最“陡”时，满足题意即可，也就是当1a时，不等式bb 32恒成立. 以下同解法一. 解法3 ：（用必要条件减少范围） 由题意得：当1a时，不等式032abab也应成立，即32 bb，解得1b（过程同解法一），此时032b，从而有32 bba对于 1a恒成立，也就是32maxbba恒成立，也就是132bb恒成立，即32 bb，得1b. 所以1m，即实数m 的最大值为1. 32 xy axy x y O m 2. 在非等腰直角ABC中，已知90C，D 是BC 的一个三等分点，若552cosBAD，求BACsin的值. 解法 1 ： 由于点 D 是BC 的三等分点，若点 D 靠近点 B ，则30BAD，即23cosBAD，又因为2352 ，所以点 D 靠近点C . 设BAD，DAC，设hACxBC,3，则 由 题 意 可 得21tan，hxhx3)tan(,tan，因为)tan(tan，所以可得2)(31221hxhx，得到1hx或31hx. 因为xh3，所以xh ，所以10103sinBAC. 综上所述，10103sinBAC. 解法 2 （代数方法）： 设bACaBC,3，运用余弦定理可得，2cos222BDADABBAD，即 2222222222222299292552abababaababADABBDADAB或者22ab . 因为ab3，从而得到ab ，又因为2293cosabaB，从而得到10103cossinBBAC. MEDACBQPMEDACBQP3. 如图，在矩形ABCD 中，EbabBCaAB),0,0(,为边BC 的中点，设QP,分别是CDBC,上的点，且满足 PECPQCDQ ，连接AQ与DP 交于点M ，...