第四章信源编码VIP免费

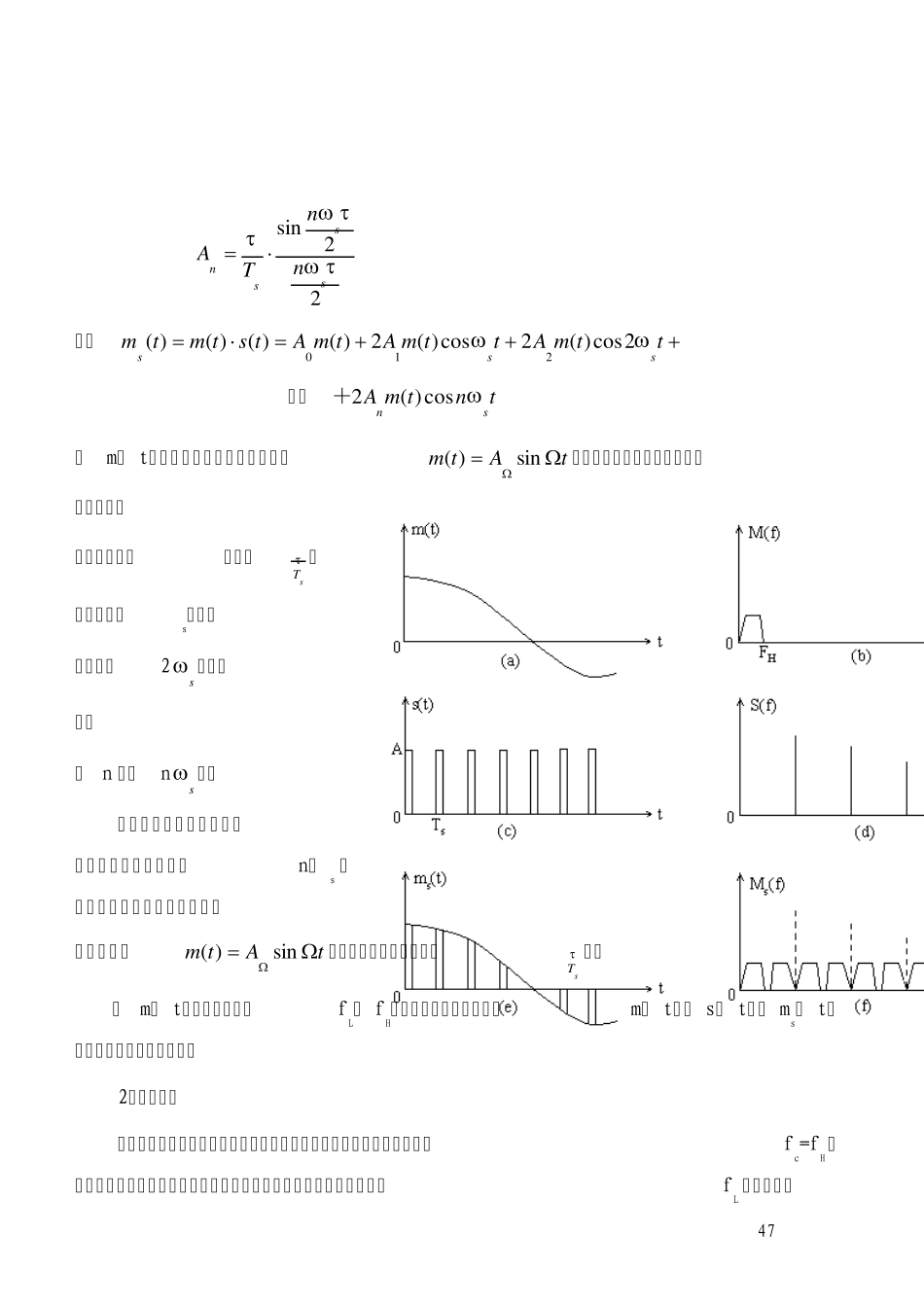
45 第四章 信源编码 一、 信源编码的作用 (1)把信源发出的模拟信号转换成以二进制为代表的数字式信息序列，完成模拟信号数字化。 (2)为了使传输更有效，把与传输内容无关的冗余信息去掉，完成信源的数据压缩。 二、 模拟信号数字化法方法 1．模拟调制 正弦波调制，调幅(AM)、调频(FM)和调相(PM)，采用的载波是正弦波，已调信号在时间上是连续的，它们均属于模拟调制。 脉冲调制，如脉冲幅度调制(PAM)、 脉冲相位调制(PPM)和脉冲宽度调制(PWM)等，虽然已调波在时间上被取样离散化了，但各自的调制参数是按照信源的规律连续地变化，所以仍然属于模拟调制的范畴。 2．模拟信号数字化法方法 模拟信号数字化的方法有很多种：脉冲编码调制（Pulse Code Modulation ，缩写为PCM）、增量调制（Delta Modulation，缩写为DM 或ΔM）、差分脉冲编码调制（缩写为DPCM）等。 脉冲编码调制(PCM)。其过程为抽样、量化、编码等，使已调波不但在时间上是离散的，且在幅度变化上用数字来体现，这便是模拟信号数字化。 4.1 抽样定理 一、抽样的概念 1．抽样的概念：抽样又可称为取样或者采样。 抽样定理是任何模拟信号数字化的理论基础。实质上，抽样定理讨论的是一个时间连续的模拟信号经过抽样变成离散序列之后，如何用这些离散序列样值不失真 46 地恢复原来的模拟信号这样一个问题。 2．抽样的任务：是对模拟信号进行时间上的离散化处理，即每隔一段时间对模拟信号抽取一个样值。 抽样是模拟信号数字化的第一步。相应的在接收端要从离散的样值脉冲不失真地恢复出原模拟信号，实现重建任务。那么，抽样脉冲的重复频率fs 必须满足什么条件才能保证收信端正确地加以重建。这就是下面要介绍的抽样定理。 二、抽样定理 1．样值信号频谱 抽样定理模型可用一个乘法器表示，如图所示。 即 ms（ t） =m（ t）〃 s（ t） 式中s（ t） 是重复周期为Ts、 脉冲幅度为1、脉冲宽度为τ的周期性脉冲序列，即抽样脉冲。如图所示。可以看出：s（ t）＝1 时，ms（ t）＝m（ t）； s（ t）＝0 时，ms（ t）＝0 下面分析样值信号频谱。S（ t）用傅立叶级数可表示为： 10cos2)(nsntnAAts 式中：sssfT22 ， sTA0 m(t) s(t) ms(t) π 47 22sinsssnnnTA 则：ttmAttmAtmAtstmtmsss2cos)(2cos)(2)()()()(210 ……tntmAsncos)(2＋ 若m（ t）为单一频率Ω的正弦...