七年级数学上册 2.8 有理数的加减混合运算 2.8.2 加法运算律在加减混合运算中的应用教学课件1 (新版)华东师大版 课件VIP免费

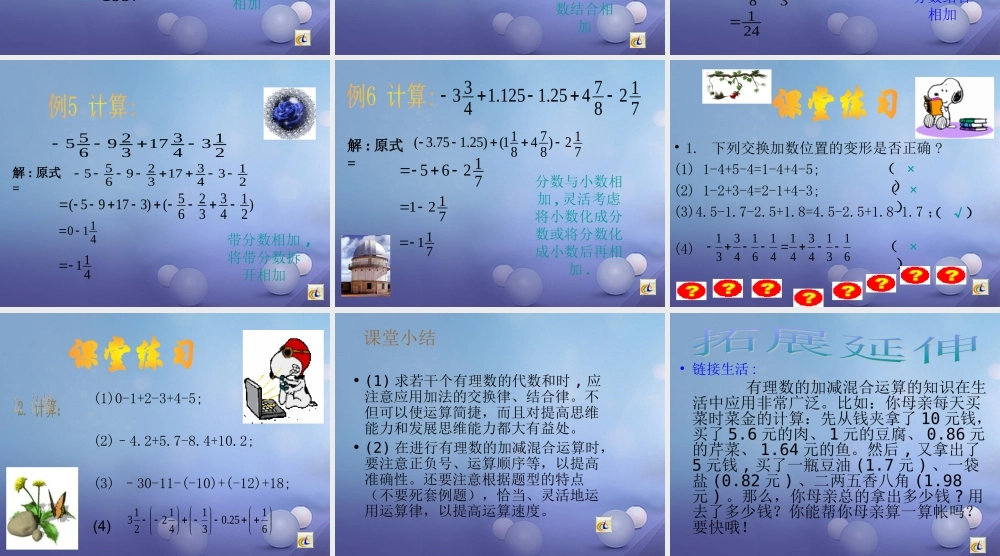
• 前面我们学过哪些有理数加法运算律？ 加法交换律： a+b=b+a 加法结合律：（ a+b ） + c=a + （ b+c ）• 恰当使用这些运算律有哪些作用？ 使运算更加简便• 联想：在有理数的加减混合运算中，是否也可以运用这些运算律？为什么？ 可以。因为有理数的加减混合运算全都可以统一成加法 .• 将正数、负数分别结合在一起： 1-2-4-7+5 (1+5)+(-2-4-7)• 将小数、整数分别结合在一起： 4.5-7+3.2+7-9 (4.5+3.2)+(-7+7-9)• 将分数、整数分别结合在一起：• 将互为相反数的结合在一起： -30+2-4-2+30 (-30+30)+(2-2)-413151254332)123()31515432(• 有理数的加减混合运算中 , 可根据题目的特点 , 简化过程 , 提高解题速度 .   3126172111解 : 原式=3126172111)316121()2711(== 20-1= 19正负数分别结合相加132199731219953211996）（）（）（）（解 : 原式=1321997312199532119961997)32312321()119951996(1997-00 1997相加得零的数结合相加15.4)382.6()6.2(3)618.0(41解 : 原式=15.4382.66.23618.041)15.46.23()382.6618.0(413107非整数相加 , 相加得整数的数结合相加323)87(432)312()21(解 : 原式=3238743231221)323312()8743221(311831241分数相加 ,同分母或分母有倍数关系的分数结合相加2134317329655解 : 原式=)21433265()31795(21343173296554110 411带分数相加 ,将带分数拆开相加解 : 原式=712)874811()25.175.3(71287425.1125.1433712657121711分数与小数相加 , 灵活考虑将小数化成分数或将分数化成小数后再相加 .• 1. 下列交换加数位置的变形是否正确 ?(1) 1-4+5-4=1-4+4-5; (2) 1-2+3-4=2-1+4-3; (3)4.5-1.7-2.5+1.8=4.5-2.5+1.8-1.7 ；(4)6131434141614331（ ×）（ ×）（ ×）（ √）(1)0-1+2-3+4-5;(2)–4.2+5.7-8.4+10.2; (3) –30-11-(-10)+(-12)+18;(4) 6125.031412213课堂小结• (1) 求若干个有理数的...