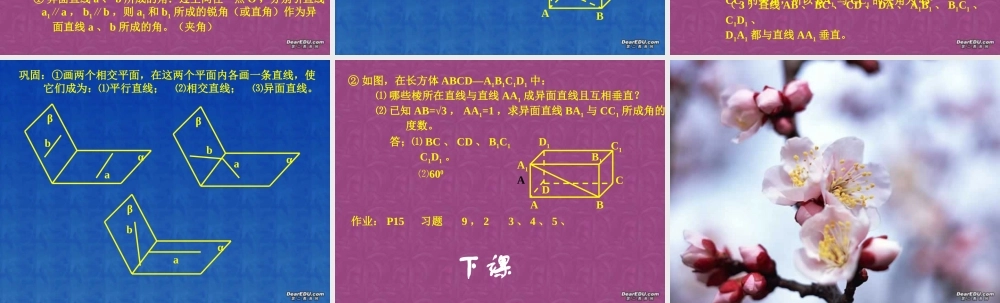
新课引入:在正方体 A1B1C1D1-ABCD 中,说出下列各对线段的位置关系ABCDA1B1C1D1( 1 ) AB 和 C1D1 ; ( 2 ) A1C1 和 AC ;( 3 ) A1C 和 D1B :( 4 ) AB 和 CC1 ;( 5 ) BD1 和 A1C1 ;空间两直线的位置关系:( 1 )从公共点的数目来看可分为: ① 有且只有一个公共点则两直线相交 两平行直线 ② 没有公共点则 两直线为异面直线( 2 )从平面的性质 来讲,可分为: 两直线相交 ① 在同一平面内 两直线平行 ② 不在同一平面内则两直线为异面直线。结论:不同在任何一个平面内的两条直线为异面直线判定异面直线的方法:( 1 )根据异面直线的定义;应用反证法来证明。( 2 )连接平面内一点与平面外一点的直线,和这个平面不经过此点的直线是异面直线。异面直线的画法:αabαabab异面直线的位置关系:αabcda 与 b 、 c 、 d 是怎样的位置关系? a 与b 、 c 、d 的位置关系都一样吗?a 与 b 、 c 、 d 都是异面直线但 a 与 b 、 c 、 d 的位置关系都不一样,其差别在两方面,一是倾斜程度不一样,如 a 、 b 间和 a 、 c 间倾斜程度不一样。二是远近程度不一样,如 a 、 d 间和 a 、 b 间的远近就不一样。① 异面直线 a 、 b 所成的角:过空间任一点 O ,分别引直线 a1a∥ , b1b∥ ,则 a1 和 b1 所成的锐角(或直角)作为异 面直线 a 、 b 所成的角。(夹角)abOa1b1ABCDA1B1C1D1思考( 1 ) AA1 与 BC 、 AA1 与 B1C1( 2 ) A1C1 与 BD 、 A1C1与 AD1所成的角是几度?② 如果两条异面直线所成的角是直角,那么我们说两条直线互 相垂直ABCDA1B1C1D1例:图中:( 1 )哪些棱所在直线与直线 BA1 是异面直线?( 2 )求直线 BA1 和 CC1 的夹角的度数( 3 )哪些棱所在直线与直线 AA1 垂直?解:( 1 )由异面直线的判定方法可 知,与直线 BA1 成异面直线的有 直线 B1C1 、 AD 、 CC1 、 DD1 、 DC D1C1 。( 2 )由 BB1CC∥1 ,可知∠ B1BA 等于异面直线 BA1与CC1 的夹角,所以 BA1 与 CC1 的夹角为 450( 3 )直线 AB 、 BC 、 CD 、 DA 、 A1B1 、 B1C1 、C1D1 、D1A1 都与直线 AA1 垂直。巩固:①画两个相交平面,在这两个平面内各画一条直线,使 它们成为:⑴平行直线; ⑵相交直线; ⑶异面直线。abαβαβbaαβba② 如图,在长方体 ABCD—A1B1C1D1 中: ⑴ 哪些棱所在直线与直线 AA1 成异面直线且互相垂直? ⑵ 已知 AB=√3 , AA1=1 ,求异面直线 BA1 与 CC1 所成角的 度数。ABCDA1AB1C1D1作业: P15 习题 9 , 2 3 、 4 、 5 、下课答;⑴ BC 、 CD 、 B1C1 C1D1 。⑵600