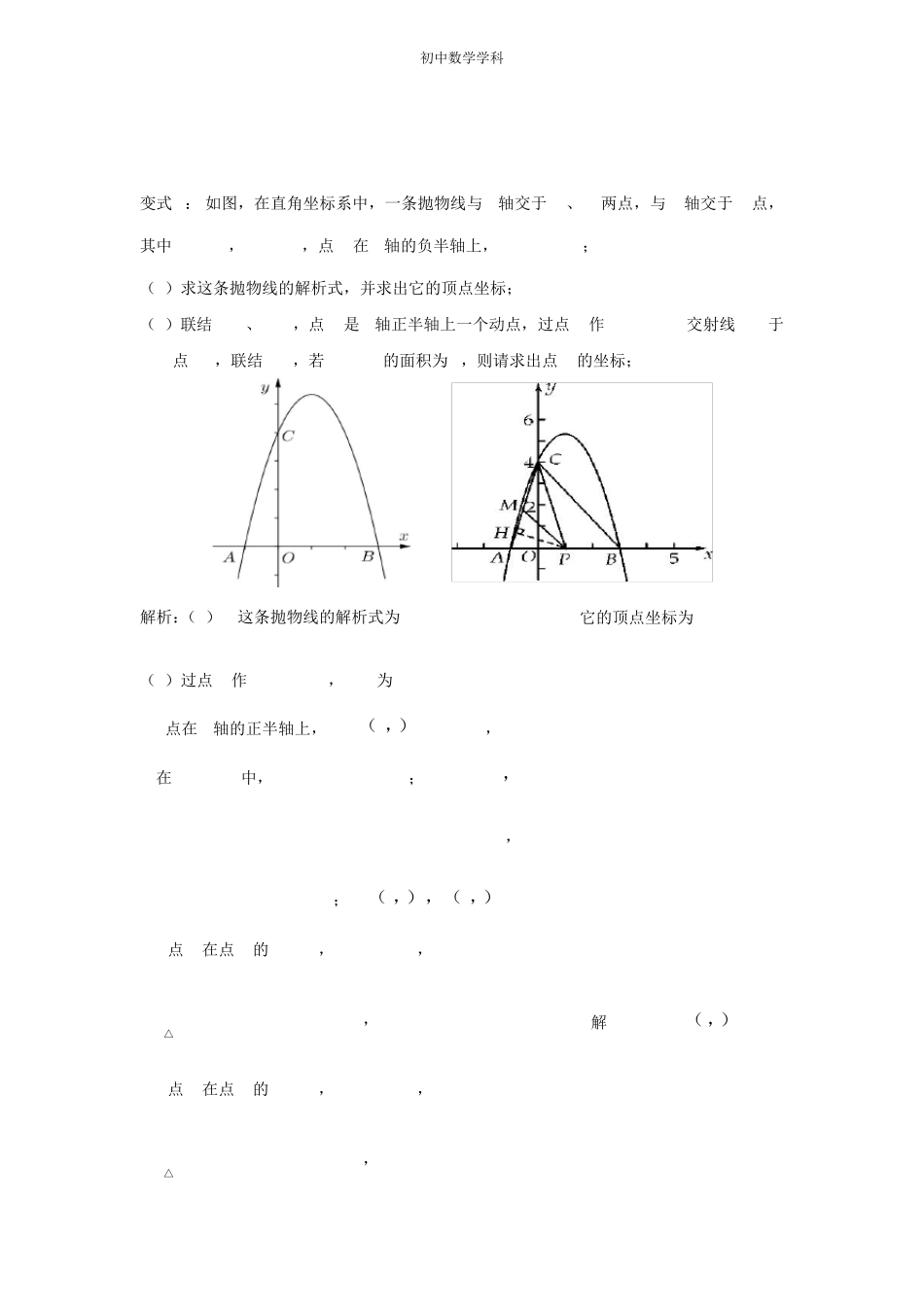
初中数学学科初中数学动点问题大全动点问题一直是中考热点题型,近几年考察探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数值、线段或面积的最值问题等,下面就此问题的常见题型作简单介绍。题型一动点形成的面积问题1.面积公式:三角形面积用12Sah来表示,利用未知数的代数式来表示底和高。2.面积比等于相似比的平方:面积无法用底和高表示时,利用相似三角形的面积比等于相似比的平方来求解,只需要知道相似比和另一个三角形面积即可表示。3.相似三角形:当面积公式和面积比等于相似比的平方不能有效解题时,利用相似三角形的比例关系求解。角度 1:利用公式法解决动点面积问题例题1:在平面直角坐标系 xOy中,抛物线2yx bxc 经过点30A( ,)和23B( ,).过点A的直线与 y轴的负半轴相交于点C,且1tan3CAO .(1)求这条抛物线的表达式及对称轴;(2)连接 AB、BC,求ABC的正切值;(3)若点D在 x轴下方的对称轴上,当ABCADCSS时,求点D的坐标.初中数学学科变式1:如图,在平面直角坐标系xOy中,已知点A的坐标为(,3)a(其中4a ),射线O与反比例函数12yx的图像交于点P,点B、C分别在函数12yx的图像上,且//AB x轴,//AC y轴.(1)当点P横坐标为6,求直线AO的表达式;(2)联结BO,当AB BO时,求点A坐标;(3)联结BP、CP,试猜想:ABPACPSS的值是否随a的变化而变化?如果不变,求出ABPACPSS的值;如果变化,请说明理由.Oxy(备用图)Oxy解析:(1) 反比例函数12yx的图像经过横坐标为6的点P,∴点P的坐标为(6,2).设直线AO的表达式为y kx(0k ).将点P(6,2)代入 y kx,解得13k .∴所求反比例函数的解析式为13yx.(2) AB//x轴,∴点B纵坐标为3,将3y 代入12yx,得4x .∴B坐标为(4,3). AB=BO,∴224(40) (30)a .解得9a .∴点A坐标为(9,3).(3)不变.延长 AB交y轴于点D,延长 AC交x轴于点E,∴32ADOAEOSSa. 点C坐标为(a,12a).∴6CEOS ,同理 6BDOS ,∴ADOBDOAEOCEOSSSS,即ABOACOSS. △ABP与△ABO同高,∴ABPABOSAPSAO.同理ACPACOSAPSAO.∴1ABPACPSS .即当a变化时,ABPACPSS的值不变,且恒为1初中数学学科变式2:如图,在直角坐标系中,一条抛物线与x轴交于A、B两点,与y轴交于C...