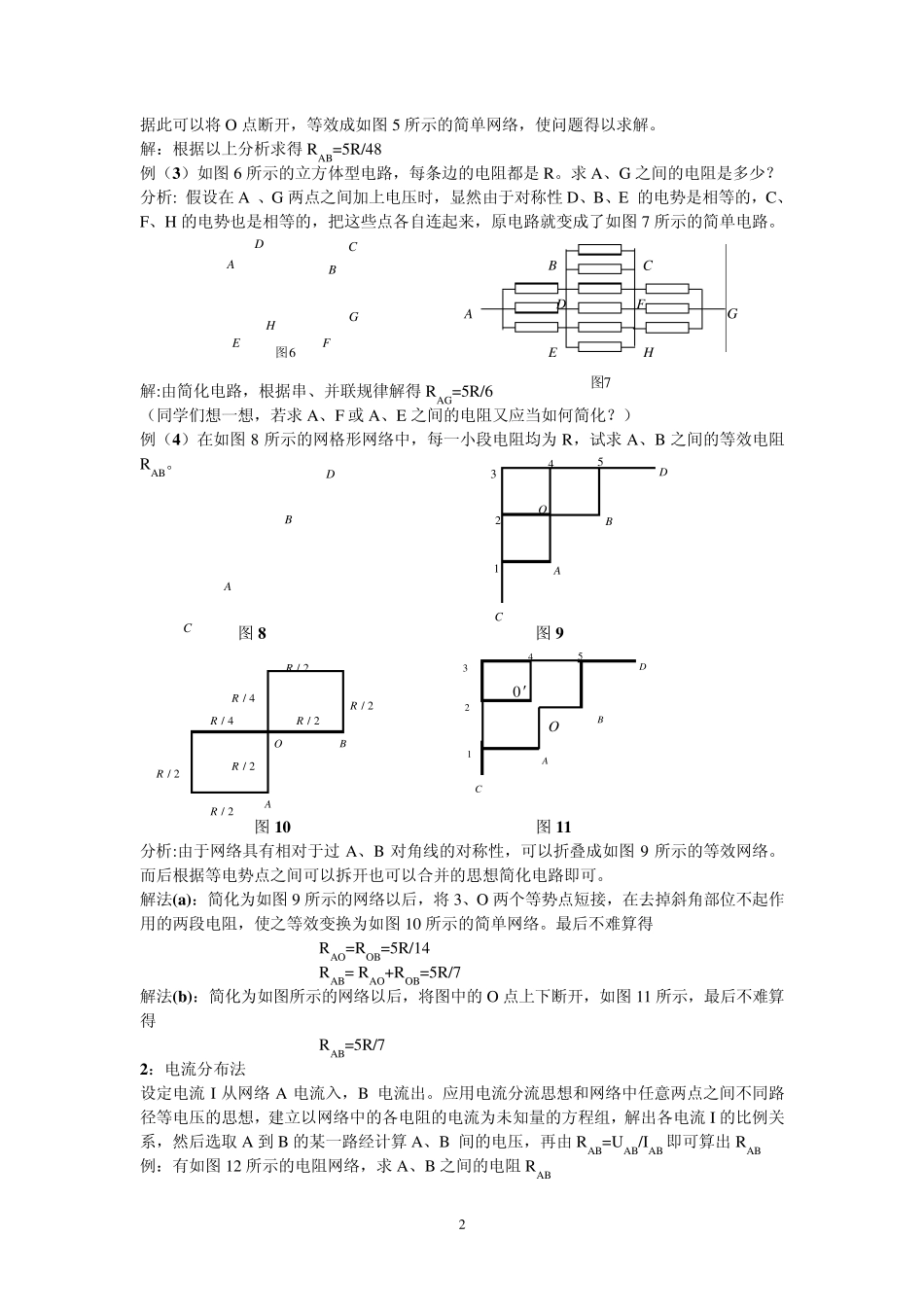
1 复杂电阻网络的处理方法 在物理竞赛过程中经常遇到,无法直接用串联和并联电路的规律求出整个电路电阻的情况,这样的电路也就是我们说的复杂电路,复杂电路一般分为有限网络和无限网络。那么,处理这种复杂电路用什么方法呢?下面,我就结合自己辅导竞赛的经验谈谈复杂电路的处理方法。 一:有限电阻网络 原则上讲解决复杂电路的一般方法,使用基尔霍夫方程组即可。它包含的两类方程出自于两个自然的结论:(1)对电路中任何一个节点,流出的电流之和等于流入的电流之和。电路中任何一个闭合回路,都符合闭合电欧姆定律。下面我介绍几种常用的其它的方法。 1:对称性简化 所谓的对称性简化,就是利用网络结构中可能存在的对称性简化等效电阻的计算。它的效果是使计算得以简化,计算最后结果必须根据电阻的串、并联公式;电流分布法;极限法等来完成。 在一个复杂的电路中,如果能找到一些完全对称的点,那么当在这个电路两端加上电压时,这些点的电势一定是相等的,即使用导线把这些点连接起来也不会有电流(或把连接这些点的导线去掉也不会对电路构成影响),充分的利用这一点我们就可以使电路大为简化。 例(1)如图 1 所示的四面体框架由电阻都为 R 的 6 根电阻丝连接而成,求两顶点 A、B 间的等效电阻。 图 1 图 2 分析:假设在 A、B 两点之间加上电压,并且电流从 A 电流入、B 点流处。因为对称性,图中 CD 两点等电势,或者说 C、D 间的电压为零。因此,CD 间的电阻实际上不起作用,可以拆去。原网络简化成简单的串、并联网络,使问题迎刃而解。 解:根据以上分析原网络简化成如图 2 所示的简单的串、并联网络,由串、并联规律得 RAB=R/2 例(2)三个相同的金属圈两两正交地连成如图所示的形状,若每一个金属圈的原长电阻为R,试求图中 A、B 两点之间的等效电阻。 图 3 图 4 图 5 分析:从图 3 中可以看出,整个电阻网络相对于 AB 的电流流入、流出方式上具有上下对称性,因此可上下压缩成如图所时的等效减化网络。从如图 4 所示的网络中可以看出,从 A点流到 O 电流与从 O 点到 B 电流必相同;从 A1 点流到 O 电流与从 O 点到 B1 电流必相同。ADBCDCABBAArrrr2/r2/r2/r2/rBABBAr2/r2/r2/r2/rrrrABO 2 据此可以将O 点断开,等效成如图5 所示的简单网络,使问题得以求解。 解:根据以上分析求得RAB=5R/48 例(3)如图6 所示的立方体型电路,每条边的电阻...