数学建模课后习题VIP免费

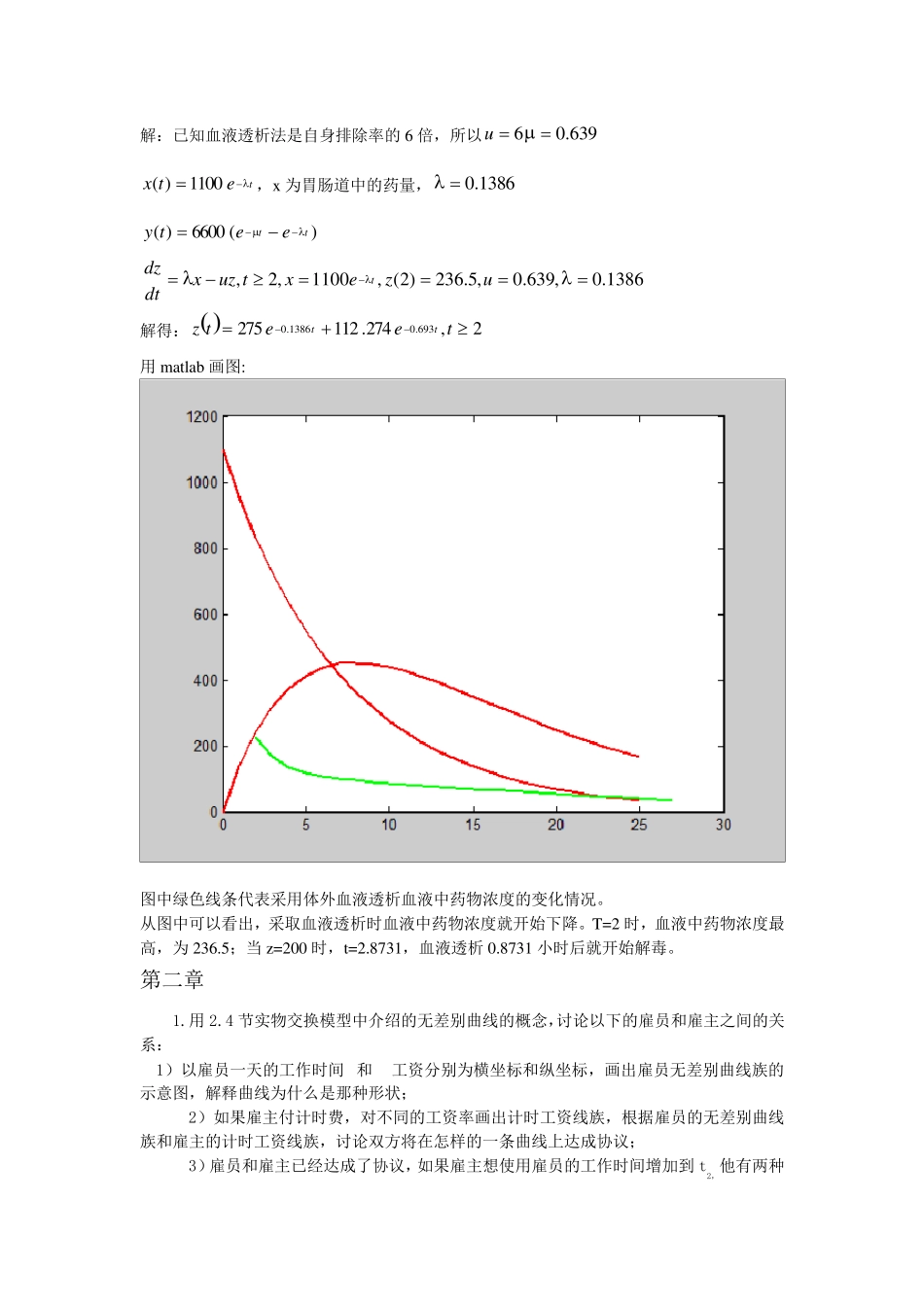
第一章 课后习题6 . 利用1.5节药物中毒施救模型确定对于孩子及成人服用氨茶碱能引起严重中毒和致命的最小剂量。 解：假设病人服用氨茶碱的总剂量为 a，由书中已建立的模型和假设得出肠胃中的药量为：)()0(mgMx 由于肠胃中药物向血液系统的转移率与药量)(tx成正比，比例系数0，得到微分方程 Mxxdtdx)0(, （1） 原模型已假设0t时血液中药量无药物，则0)0(y，)(ty的增长速度为 x 。由于治疗而减少的速度与)(ty本身成正比，比例系数0，所以得到方程： 0)0(,yyxdtdy （2） 方程（1）可转换为：tMetx)( 带入方程（2）可得：)()(tteeMty 将01386和1155.0带入以上两方程，得： tMetx1386.0)( )(6)(13866.01155.0eeMtyt 针对孩子求解，得： 严重中毒时间及服用最小剂量：ht876.7，mgM87.494； 致命中毒时间及服用最小剂量：ht876.7，mgM8.4694 针对成人求解： 严重中毒时间及服用最小剂量：ht876.7，mgM83.945 致命时间及服用最小剂量：ht876.7，mgM74.1987 课后习题7 . 对于1.5 节的模型，如果采用的是体外血液透析的办法，求解药物中毒施救模型的血液用药量的变化并作图。 解：已知血液透析法是自身排除率的6 倍，所以639.06 u tetx 1100)(，x 为胃肠道中的药量，1386.0 )(6600)(tteety 1386.0,639.0,5.236)2(,1100,2,uzextuzxdtdzt 解得： 2,274.112275693.01386.0teetztt 用matlab 画图: 图中绿色线条代表采用体外血液透析血液中药物浓度的变化情况。 从图中可以看出，采取血液透析时血液中药物浓度就开始下降。T=2 时，血液中药物浓度最高，为236.5；当 z=200 时，t=2.8731，血液透析0.8731 小时后就开始解毒。 第二章 1.用2.4 节实物交换模型中介绍的无差别曲线的概念，讨论以下的雇员和雇主之间的关系： 1）以雇员一天的工作时间 和工资分别为横坐标和纵坐标，画出雇员无差别曲线族的示意图，解释曲线为什么是那种形状； 2）如果雇主付计时费，对不同的工资率画出计时工资线族，根据雇员的无差别曲线族和雇主的计时工资线族，讨论双方将在怎样的一条曲线上达成协议； 3）雇员和雇主已经达成了协议，如果雇主想使用雇员的工作时间增加到 t2，他有两种办法：一是提高计时工资率，在协议线的另一点 达成新的协议；二是实行...