浅谈矩阵的LU分解和QR分解及其应用VIP免费

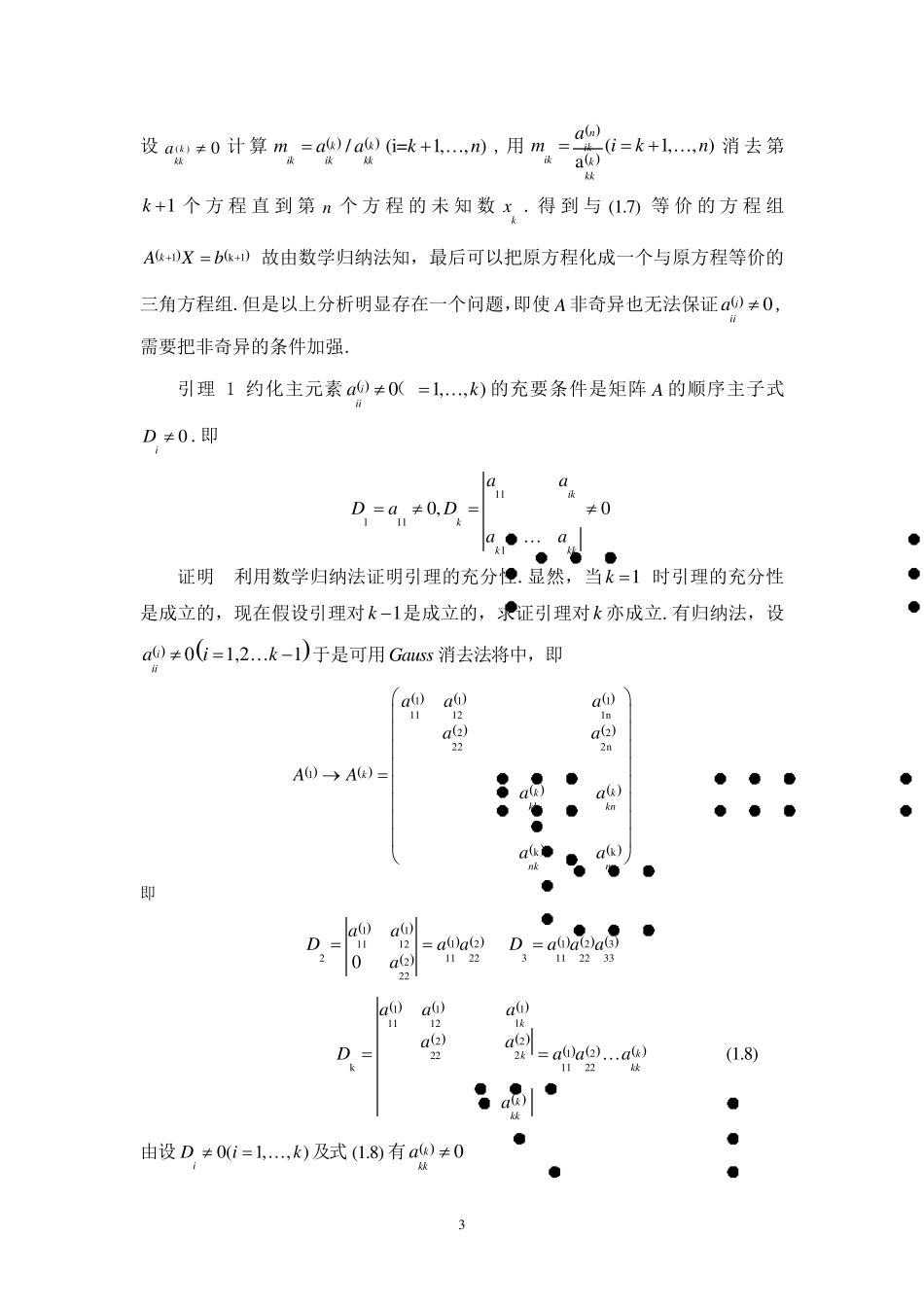
1 浅谈矩阵的LU 分解和QR 分解及其应用 基于理论研究和计算的需要，往往有必要把矩阵分解为具有某种特性的矩阵之积，这就是我们所说的矩阵分解. 本文将介绍两种常用的矩阵分解方法，以及其在解线性方程组及求矩阵特征值中的应用. 1 .矩阵的LU 分解及其在解线性方程组中的应用 1 .1 高斯消元法 通过学习，我们了解到利用Gauss 消去法及其一些变形是解决低阶稠密矩阵方程组的有效方法.并且近些年来利用此类方法求具有较大型稀疏矩阵也取得了较大进展.下面我们就通过介绍Gauss 消去法，从而引出矩阵的LU 分解及讨论其对解线性方程组的优越性. 首先通过一个例子引入： 例 1,解方程组 (1 .1 )(1 . 2 )(1 .3 ) 解. 1Step (1 .1 )( 2 )(1 .3 )  消去(1 .3 ) 中未知数,得到 2341 1xx  (1 .4 ) 2Shep . (1 .2 )(1 .4 ) 消去(1 .4 ) 中的未知数2x 有12323364526xxxxxx   显然方程组的解为*x 123      上述过程相当于 111604152211111604150411111604150026 2（）+ ()iir表示矩阵的行 2 由此看出，消去法的基本思想是：用逐次消去未知数的方法把原方程化为与其等价的三角方程组. 下面介绍解一般n 阶线性方程组的Gauss 消去法. 设111nn 1n naaaaA  1n xXx  1nbbb  则 n 阶线性方程组 AXb (1.5) 并且 A为非奇异矩阵 . 通过归纳法可以将 AXb化为与其等价的三角形方程，事实上： 及方程(1.5) 为  11A Xb,其中  1AA  1bb (1) 设(1)110a，首先对行计算乘数  11i1111iamm.用1im乘(1.5) 的第一个方程加到第 2,3,,i in个方程上.消去方程(1.5) 的第 2 个方程直到第 n 个方程的未知数1x .得到与(1.5) 等价的方程组   11n12n111n n0aaxxa  112nbb简记作   22Ab (1.6) 其中      211211111 ijijiijiiiambbmaab (2) 一般第 11kkn  次消去，设第1k  步计算完成.即等价于   kkAXb...