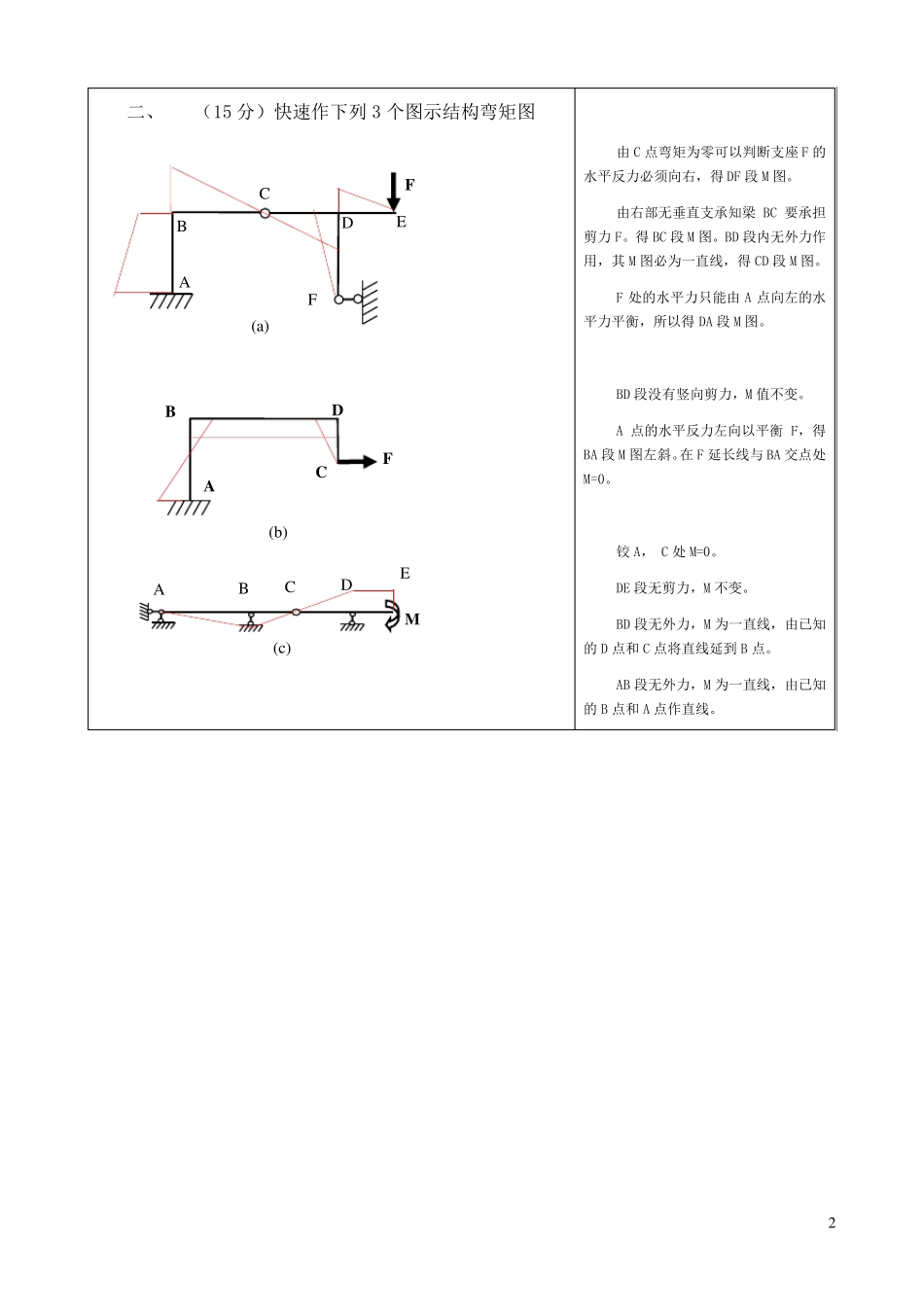
1 一、 (6 分)图示结构是 多余约束的几何 变体系(简述分析过程) 解:先计算体系的计算自由度W 如果以结点为观察对象:W = 2j – b = 2×6-16 =0 以刚片为对象:W = 3m-2j-b = 3×12 – 2×16 – 4 =0 以三角形组成的不变体系I 和 II 加大地为III 组成三刚片体系。刚片 1 和 2 以二平行的连杆组成平行于地面的无穷远处虚铰,实铰(1,3)和(2,3)与此无穷远虚铰不成一线,因而体系为几何不变。 由于 W=0,所以本体系为无多余约束的几何不变体系。 此题应先计算W,再分析是否几何可变。如果W>0, 则一定为几何可变;如果W=0,则无多余约束;如果W<0,则有多余约束。 I II III 1,3 2,3 1,2 2 二、 (15 分)快速作下列 3 个图示结构弯矩图 由 C 点弯矩为零可以判断支座 F 的水平反力必须向右,得 DF 段 M 图。 由右部无垂直支承知梁 BC 要承担剪力 F。得 BC 段 M 图。BD 段内无外力作用,其 M 图必为一直线,得 CD 段 M 图。 F 处的水平力只能由 A 点向左的水平力平衡,所以得 DA 段 M 图。 BD 段没有竖向剪力,M 值不变。 A 点的水平反力左向以平衡 F,得BA 段 M 图左斜。在 F 延长线与 BA 交点处M=0。 铰 A, C 处 M=0。 DE 段无剪力,M 不变。 BD 段无外力,M 为一直线,由已知的 D 点和 C 点将直线延到 B 点。 AB 段无外力,M 为一直线,由已知的 B 点和 A 点作直线。 (a) F A B C D F E (b) F A B D C (c) M A B C D E 3 45kN/m A C 6m 2m B 45kN/m M 1 A C B M 2 三、 (10 分)已知 EI = 3.15×1010kNmm2, 求图示等截面梁C 点的竖向位移 解: 1、先求支座反力,然后根据支座反力作荷载下的弯矩图 kNFFBA1352645 kNmAFM5.2025.2023135223453max 2、为求梁 C 点处的竖向位移,在 C 点处施加一竖向单位力。求单位力作用下的支座反力,并由此做出单位力作用下的弯矩图 M 。 3、根据求位移的单位力法 )(0257.00101015.36)05.2022(26610 mdxEIMMdxEIMMdxEIMMCBBAVC 故 C 点的竖向位移为 25.7mm,方向向上。 简支梁的跨中弯矩可直接由82maxqlM求得 一般情况下是需要先求的反力然后再作弯矩图的,然而在很多情况下单位力作用下的弯矩图可以不通过求反力直接作出,本例即是如此...