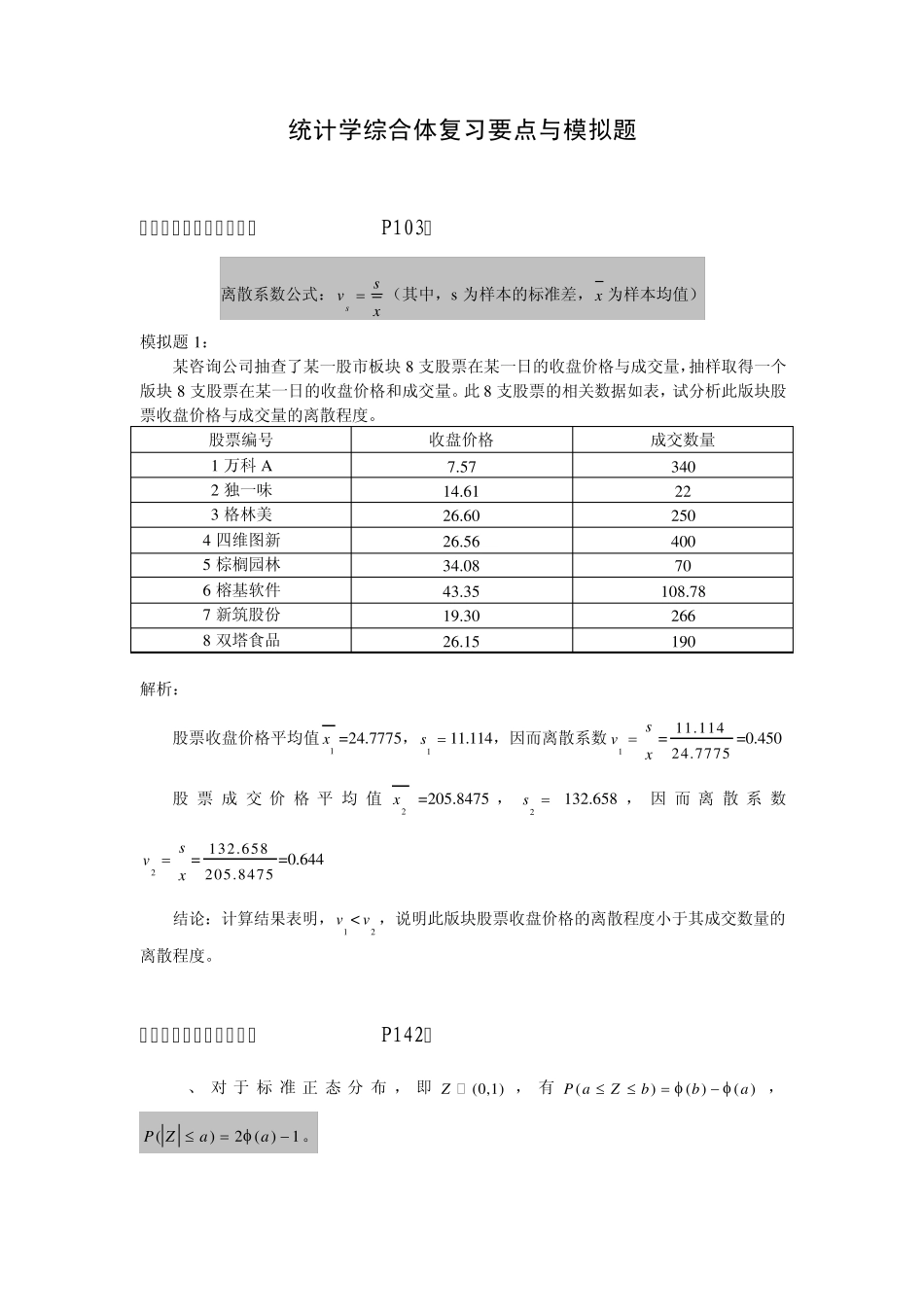
统计学综合体复习要点与模拟题 考查要点一、离散系数(P103) 离散系数公式:ssvx(其中,s为样本的标准差,x 为样本均值) 模拟题1: 某咨询公司抽查了某一股市板块8 支股票在某一日的收盘价格与成交量,抽样取得一个版块8 支股票在某一日的收盘价格和成交量。此8 支股票的相关数据如表,试分析此版块股票收盘价格与成交量的离散程度。 股票编号 收盘价格 成交数量 1 万科A 7.57 340 2 独一味 14.61 22 3 格林美 26.60 250 4 四维图新 26.56 400 5 棕榈园林 34.08 70 6 榕基软件 43.35 108.78 7 新筑股份 19.30 266 8 双塔食品 26.15 190 解析: 股票收盘价格平均值1x =24.7775,1s 11.114,因而离散系数1vsx= 11.11424.7775=0.450 股票成交价格平均值2x=205.8475 ,2s132.658 ,因而离散系数2vsx= 132.658205.8475=0.644 结论:计算结果表明,1v <2v ,说明此版块股票收盘价格的离散程度小于其成交数量的离散程度。 考查要点二、正态分布(P142) 1、 对 于标准正 态 分布 ,即(0,1)Z ,有()( )( )P aZbba,()2 ( )1P Zaa 。 2、对于负 z ,可由()1( )zz得到。 3、对于一般正态分布,即(,)X ,有 ()baP aXb ()()xP Xx 模拟题 2: 一工厂生产的电子管寿命 X (以小时计算)服从期望值 =160 的正态分布,若要求1202000.08Px,允许标准差 最大为多少? 解析: 电子管寿命 X 服从 N(160,2),为一般正态分布,经过标准化成为标准正态分布,即X -160(0,1),由此, 120200Px=120160160200160XP=4016040XP=16040XP 而16040XP=240()-1 因此,如果 1202000.08Px,要求 240()-1 0.08,计算得40() 0.54,查表(P446),概率 0.54 对应的分位数为 0.1004,即 (0.1004)=0.54, 所以,只要满足 40 0.1004,计算得 398.406,即允许的 的最大值。 模拟题 3: 一本书排版后一校时出现错误次数 X 服从正态分布 N(200,400),求 (1) 出现错误次数不超过 230 的概率。 (2) 出现错误次数在 190-210 之间的概率。 解析: X 服从正态...