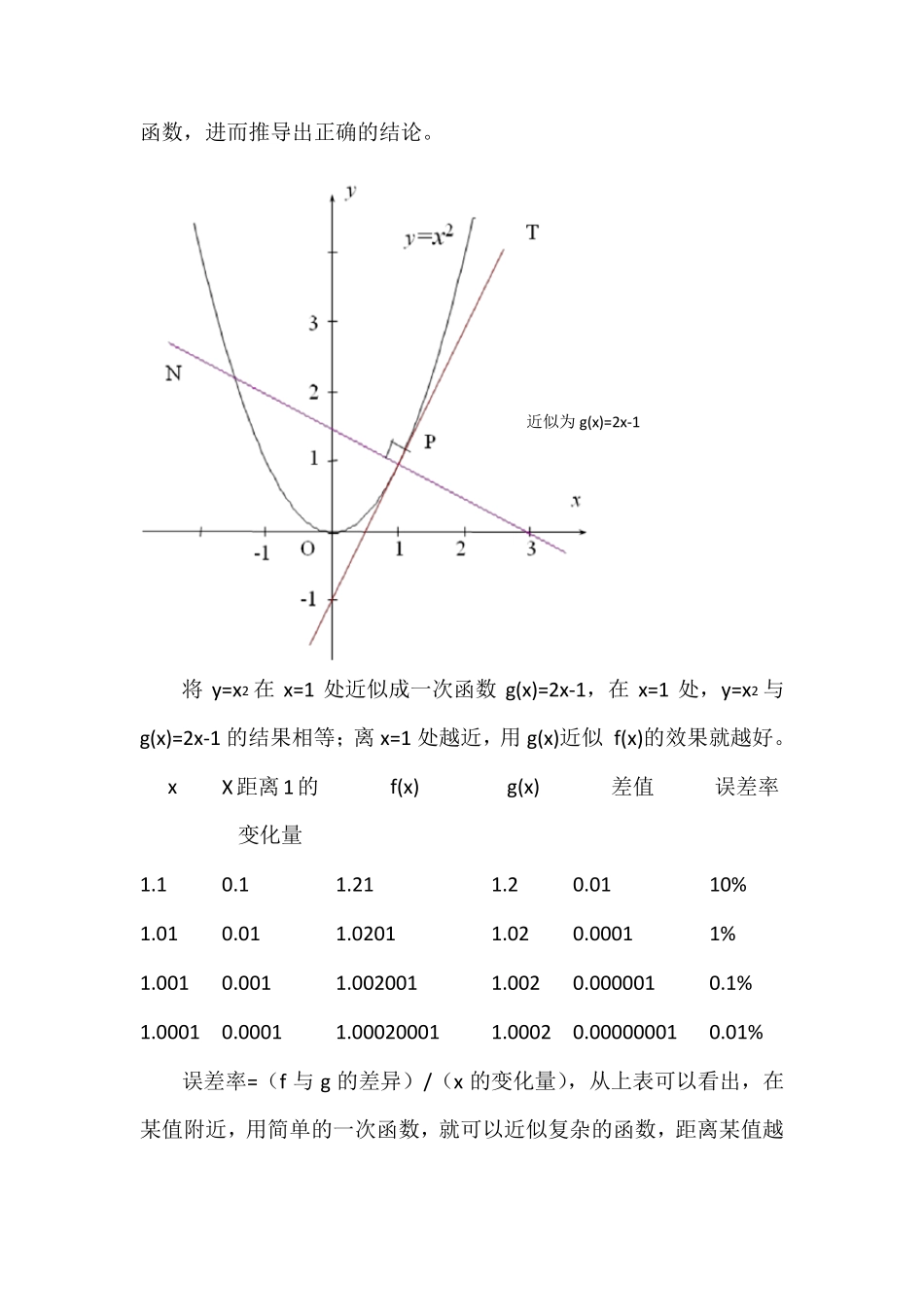
导数基础讲义 导数是微积分的核心概念之一它是研究函数增减、变化快慢、最大(小)值等问题最一般、最有效的工具。 导数研究的问题即变化率问题:研究某个变量相对于另一个变量变化的快慢程度. 序章 函数 一件事变成了这样,使得另一件事变成了那样。所谓函数,说的就是事物间的相关性,函数说到底就是用来描述“关系”(或因果)“变化”或者“单位变化”的工具。 y=f(x) 就是使用f 给 x 施加某种规则或关系,进而推导出 y。 例:声速和气温可以用函数表示,每上升 1℃,声速就会提高0.6m/s,y=0.6x+331。 温度为 15℃时,声速=0.6x15+331=340m/s 例:将华氏温度x(℉)变换为摄氏温度y(℃),y=(x-32)*5/9 x=50℉时,y=(50-32)*5/9=10℃; x=68℉时,y=(68-32)*5/9=20℃ 第一章 微分就是将函数化繁为简 在讨论局部性质时,可以使用简单的一次函数来替代复杂的原函数,进而推导出正确的结论。 将 y=x2 在 x=1 处近似成一次函数g(x)=2x-1,在 x=1 处,y=x2 与g(x)=2x-1 的结果相等;离 x=1 处越近,用 g(x)近似 f(x)的效果就越好。 x X距离1的变化量 f(x) g(x) 差值 误差率 1.1 0.1 1.21 1.2 0.01 10% 1.01 0.01 1.0201 1.02 0.0001 1% 1.001 0.001 1.002001 1.002 0.000001 0.1% 1.0001 0.0001 1.00020001 1.0002 0.00000001 0.01% 误差率=(f 与 g 的差异)/(x 的变化量),从上表可以看出,在某值附近,用简单的一次函数,就可以近似复杂的函数,距离某值越近似为 g(x)=2x-1 近,近似的效果越好。所谓近似成一次函数,就是令原函数的误差率为0 的情况。 在x=x0 处,用来近似f(x)的一次函数g(x)=kx+b,其中,k 被称为f(x) 在x=x0 处的微分系数,k=f’(x0),就是y= f(x)在x=x0 处切线的斜率。 由y=f(x)求解导函数 的过程称为微分 求几个常用的函数的导数: 1、函数( )yf xc的导数 根据导数定义,因为 ()( )0yf xxf xccxxx 所以00limlim 00xxyyx 函数 导数 yc 0y 0y 表示函数yc图像(图 3.2-1)上每一点处的切线的斜率都为0.若 yc表示路程关于时间的函数,则0y 可以解释为某物体的瞬时速度始终为0,即物体一直处于静止状态. 2.函数( )yf xx的导数 因为 ()( )1yf xxf xxxxxxx 所以00limlim 11xxyyx ...