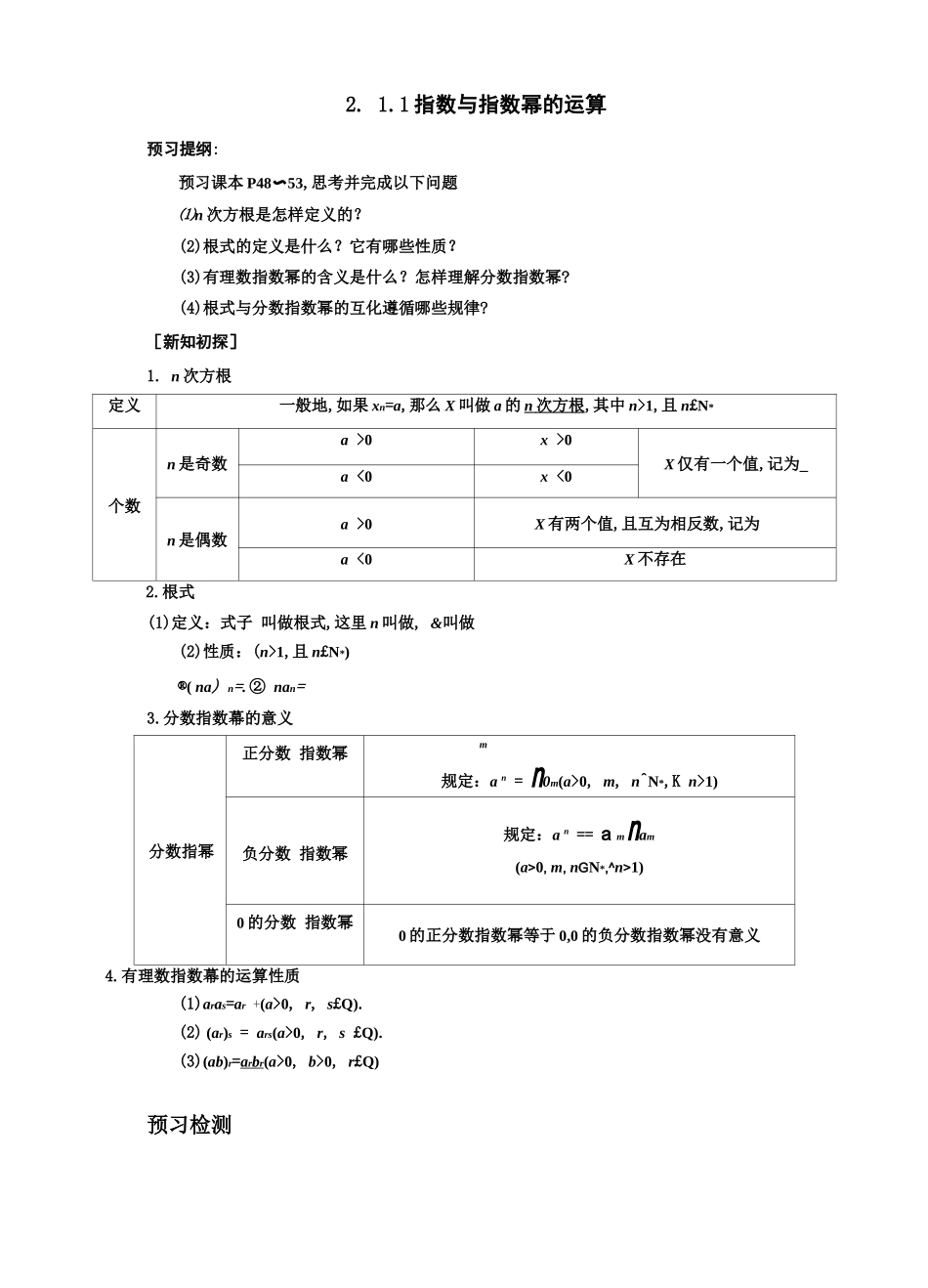
2. 1.1 指数与指数幂的运算预习提纲:预习课本 P48〜53,思考并完成以下问题⑴n 次方根是怎样定义的?(2)根式的定义是什么?它有哪些性质?(3)有理数指数幂的含义是什么?怎样理解分数指数幂?(4)根式与分数指数幂的互化遵循哪些规律?[新知初探]1. n 次方根定义一般地,如果 xn=a,那么 X 叫做 a 的 n 次方根 ,其中 n>1,且 n£N*个数n 是奇数a >0x >0X 仅有一个值,记为_a <0x <0n 是偶数a >0X 有两个值,且互为相反数,记为a <0X 不存在2.根式(1)定义:式子 叫做根式,这里 n 叫做, &叫做(2)性质:(n>1,且 n£N*)®( na) n=. ② nan=3.分数指数幕的意义分数指幂正分数 指数幂m规定:a n = n0m(a>0, m, n^N*,K n>1)负分数 指数幂规定:a n == a m nam(a>0, m, nGN*,^n>1)0 的分数 指数幂0 的正分数指数幂等于 0,0 的负分数指数幂没有意义4.有理数指数幕的运算性质(1)aras=ar +(a>0, r, s£Q).(2) (ar)s = ars(a>0, r, s £Q).(3)(ab)r=a r b r (a>0, b>0, r£Q)预习检测1 .判断(正确的打“J〞,错误的打“义〞)(1)任意实数的奇次方根只有一个.()(2)正数的偶次方根有两个且互为相反数.()(3) m;(n-4)2=4-n.() (4)分数指数幂 a n可以理解为?个 a 相乘.()(5)0 的任何指数幂n都等于 0.()2 .处心可化为() 2525A. a 飞 B. a 2C. a 5D..—a 233 .化简 25 2的结果是()A. 5 B. 15C. 25 D. .1254 .计算:no+2-2 X 1^24)2 =.课堂案根式的化简与求值[例 1]化简:[活学活用]1.假设 xyW0,那么使/4x2y2=-2xy 成立的条件可能是()A. x>0, y>0B. x>0, y<0C. x20, y20D. x<0, y<02.假设、J(2a-1)2=弋(1-2a)3,那么实数 a 的取值范围为[例 2]用分数指数幂的形式表示以下各式(式中字母都是正数):[活学活用]型二(1)n(x—n)n(x0) B.6'y2=y 1(y<0) C.x—3=yC)(x>0) D.x—1= — 3X(xW0)4 .将以下根式与分数指数幂进行互化:a 3③(a >0).7 a • 5 a4[例 3]计算以下各式:(1)(23)0+2—2义 04)—2 —0.010.5;(2) 0.064 -3 —[活学活用]5 .计算:(1)0.027; —G) 2 +2563 +(2近)3 —3—1+ 加;(2)(2) (a—必—3)-(—4a—必)4(12a—必—曲);[一题多变]②?;a、;a(a>0);指数幂的运算—[).+[( —2)3] -3 +16—0.75;题型四条件求值问题腰琏发做[例 4]a 21+a -2 =,,5 求以下各式的值:(1) a+a—1;(2)a2+a—2.1.[变结论]在本例条件下,那么 02—a-2=.课后检测:1.以下各式既符合分数指数幂的定义,值又相等的是〔〕11_211 i3.1、A. 〔—1〕3和〔一 1〕6B. 0-2和 02 C. 22和 44 D. 4-2 和〔jJ-32 .:n£N, n>1,那么气:(一 5>等于()A. 5B.-5C.-5 或 5D.不能确定3 ~ - 43 .化简[3〞一 5)2]的结果为()