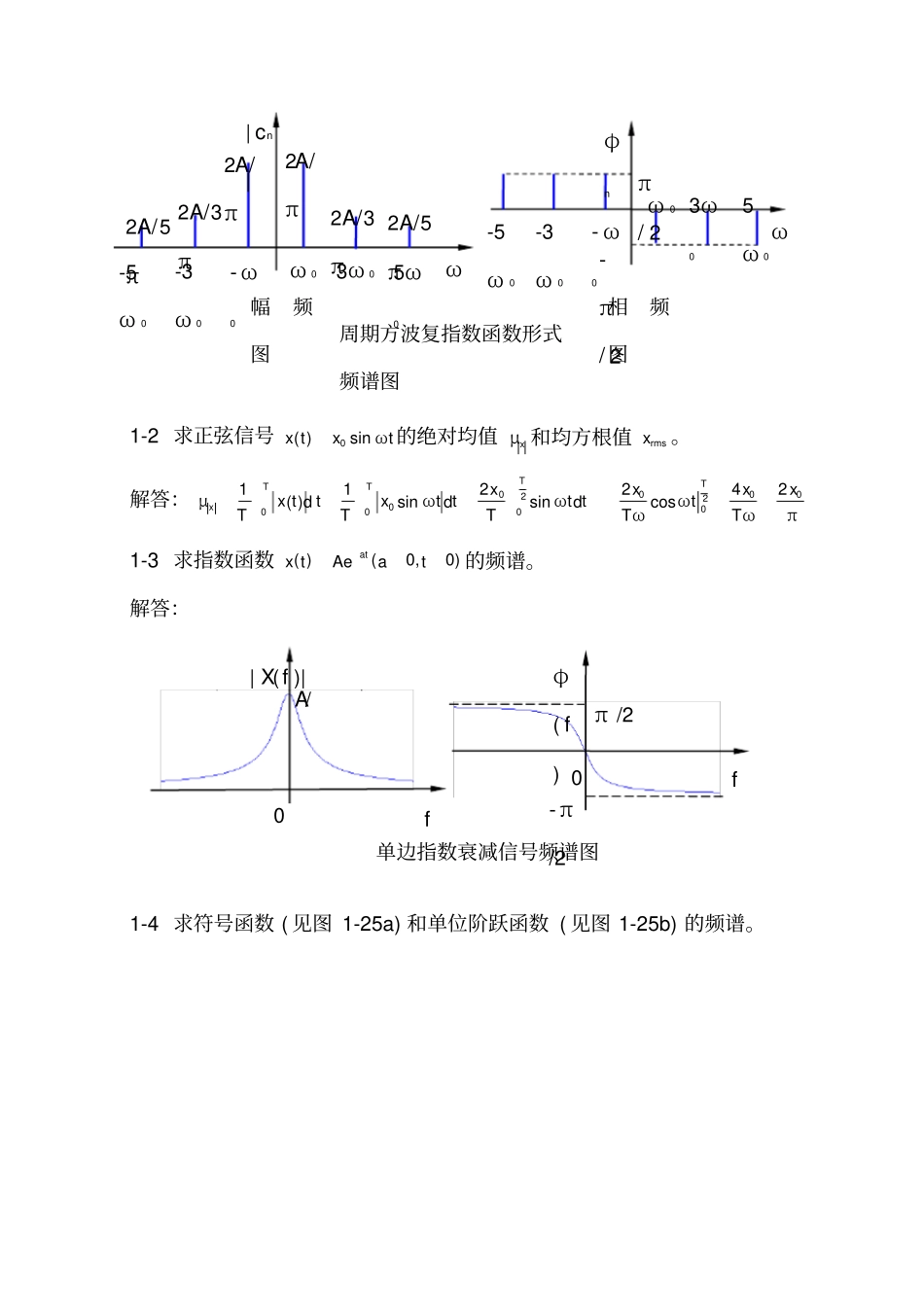
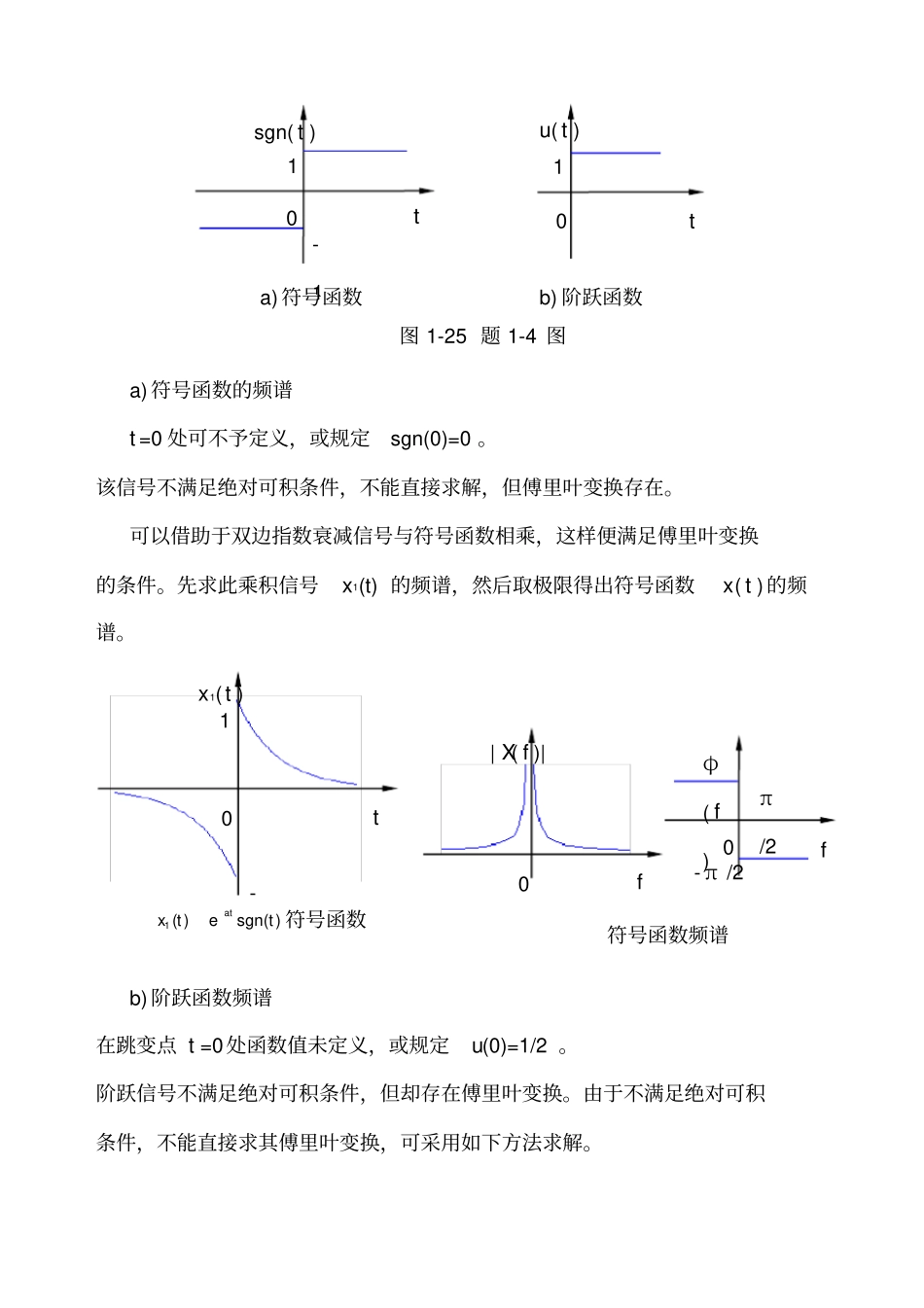
机 械 工 程 测 试 技 术 基 础 习 题 解 答第一章信号的分类与描述1-1 求周期方波(见图 1-4 )的傅里叶级数 (复指数函数形式),划出| cn|– ω 和φ n– ω 图,并与表 1-1 对比。解答:在一个周期的表达式为00 (0)2( ) (0)2TAtx tTAt. 积分区间取( -T/2 ,T/2 )所以复指数函数形式的傅里叶级数为001( )(1cos)jntjntnnnAx tc ejnen,=0, 1, 2, 3, nL 。没有偶次谐波。其频谱图如下图所示。图 1-4 周期方波信号波0 t x(⋯⋯A -A 1-2 求正弦信号0( )sinx txωt 的绝对均值xμ 和均方根值rmsx。解答:00002200000224211( )dsindsindcosTTTTxxxxxμx ttxωt tωt tωtTTTTωTωπ1-3 求指数函数( )(0,0)atx tAeat的频谱。解答:1-4 求符号函数 ( 见图 1-25a) 和单位阶跃函数 ( 见图 1-25b) 的频谱。单边指数衰减信号频谱图f | X(f )| A/0 φ( f) f 0 π /2 - π/2 | cn| φn π/ 2 -π/ 2 ωωω 0ω 03ω 05ω03ω05ω 02A/π2A/3π2A/5π幅频图相频图周期方波复指数函数形式频谱图2A/5π2A/3π2A/π- ω0-3ω 0-5ω 0- ω0-3ω 0-5ω 0a) 符号函数的频谱t =0 处可不予定义,或规定sgn(0)=0 。该信号不满足绝对可积条件,不能直接求解,但傅里叶变换存在。可以借助于双边指数衰减信号与符号函数相乘,这样便满足傅里叶变换的条件。先求此乘积信号x1(t) 的频谱,然后取极限得出符号函数x( t )的频谱。b) 阶跃函数频谱在跳变点 t =0处函数值未定义,或规定u(0)=1/2 。阶跃信号不满足绝对可积条件,但却存在傅里叶变换。由于不满足绝对可积条件,不能直接求其傅里叶变换,可采用如下方法求解。1( )sgn( )atx tet 符号函数t x1(t ) 0 1 -符号函数频谱f φ( f) 0 π/2 0 f | X( f )| - π /2 t sgn( t ) 0 1 -1 t u( t ) 0 1 图 1-25 题 1-4 图a) 符号函数b) 阶跃函数解法 1:利用符号函数结果表明, 单位阶跃信号 u( t ) 的频谱在 f =0 处存在一个冲激分量, 这是因为u( t )含有直流分量,在预料之中。同时,由于u( t ) 不是纯直流信号,在t =0处有跳变,因此在频谱中还包含其它频率分量。解法 2:利用冲激函数根据傅里叶变换的积分特性1-5 求被截断的余弦函数0cosω t ( 见图 1-26) 的傅里叶变换。0cos( )0ω ttTx ttT解:0( )( )cos(2)x tw tf tw( t...