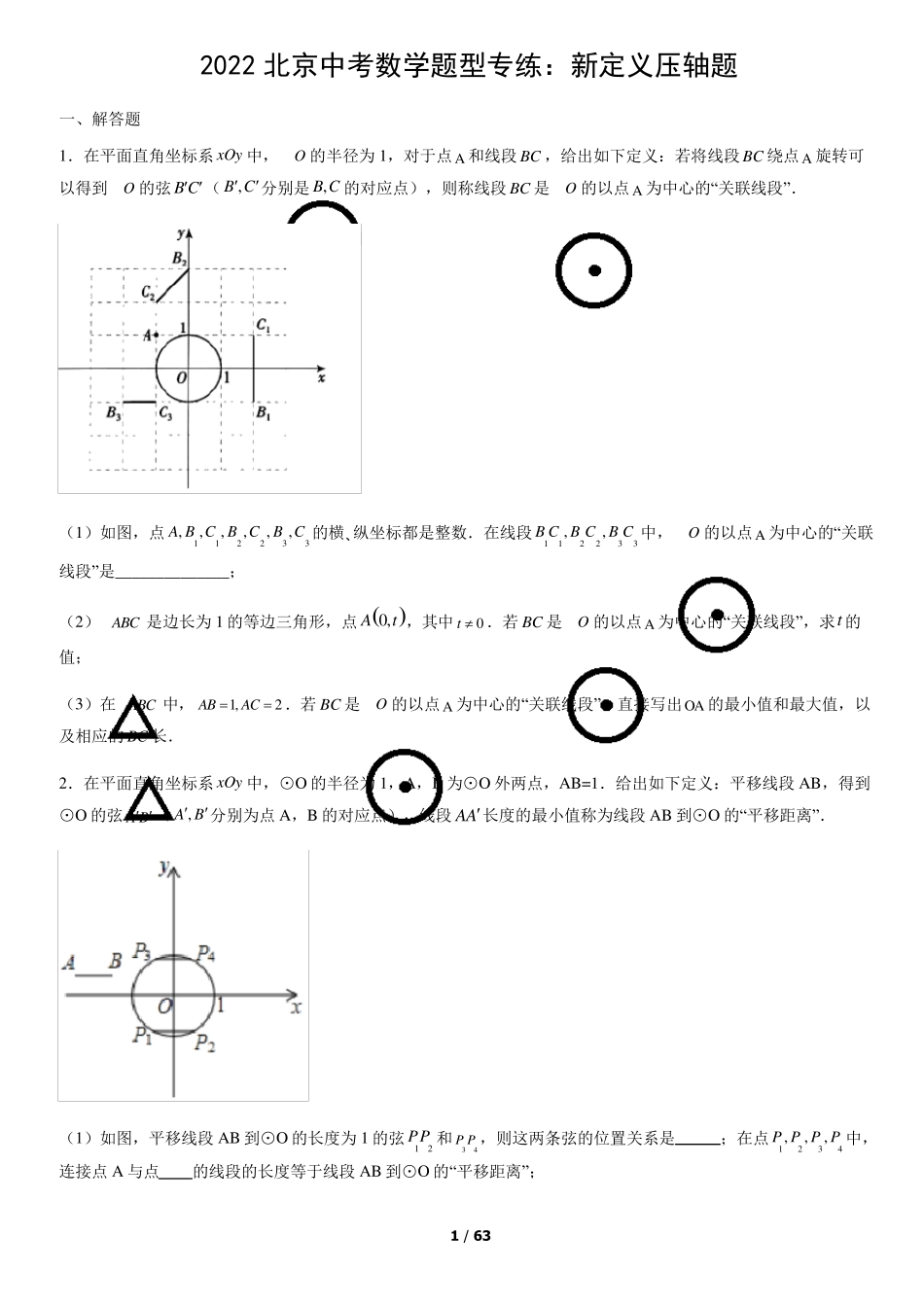
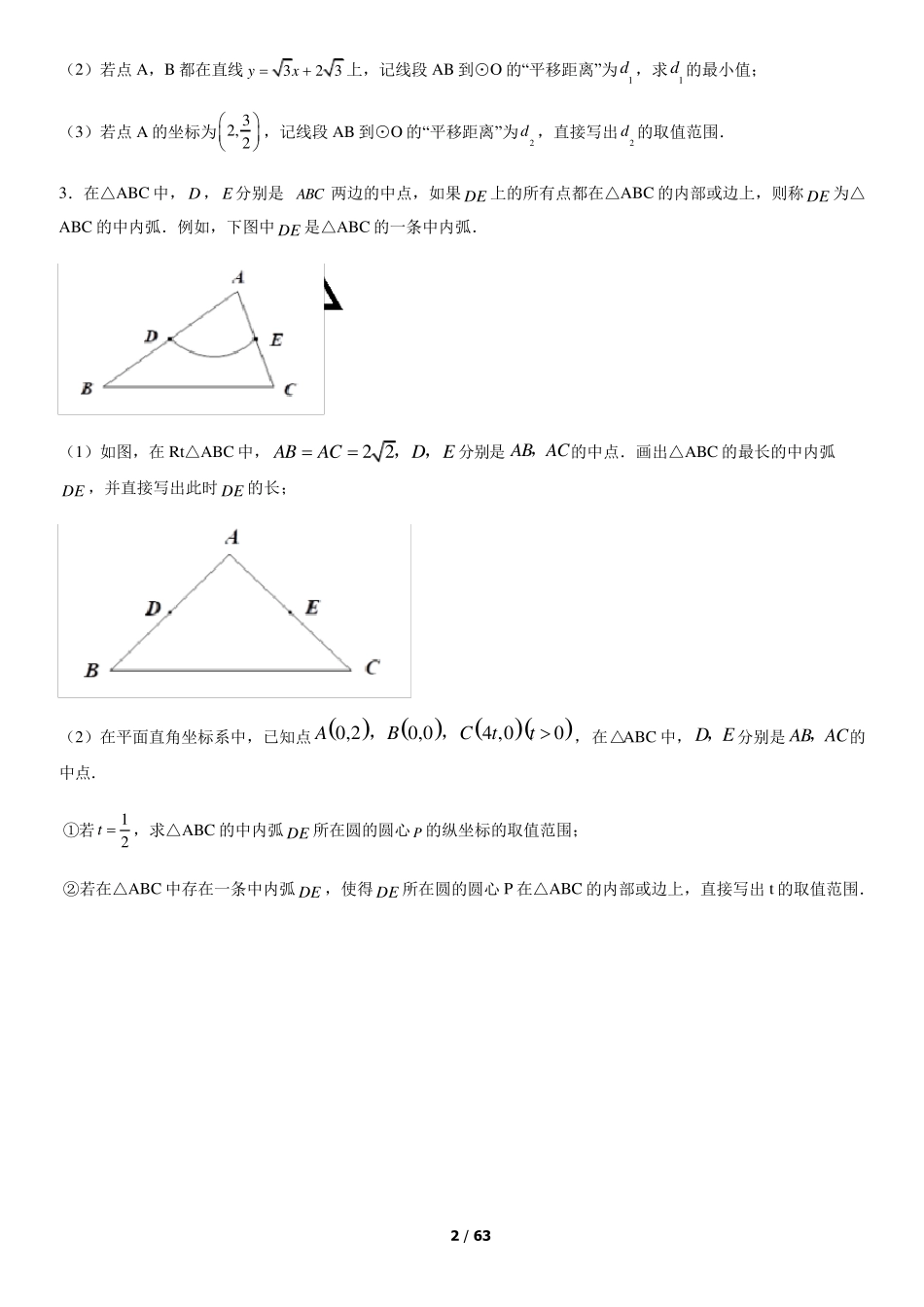
1 / 63 2022 北京中考数学题型专练:新定义压轴题 一、解答题 1.在平面直角坐标系x Oy 中,O 的半径为1,对于点A 和线段BC ,给出如下定义:若将线段BC 绕点A 旋转可以得到O 的弦B C (,B C分别是,B C 的对应点),则称线段BC 是O 的以点A 为中心的“关联线段”. (1)如图,点112233,,,,,,A B C B CB C 的横、纵坐标都是整数.在线段112233,,B C B CB C 中,O 的以点A 为中心的“关联线段”是______________; (2)ABC 是边长为1 的等边三角形,点0,At ,其中0t .若BC 是O 的以点A 为中心的“关联线段”,求t 的值; (3)在ABC 中,1,2ABAC .若BC 是O 的以点A 为中心的“关联线段”,直接写出OA 的最小值和最大值,以及相应的BC 长. 2.在平面直角坐标系x Oy 中,⊙O 的半径为1,A,B 为⊙O 外两点,AB=1.给出如下定义:平移线段AB,得到⊙O 的弦A B (,A B分别为点A,B 的对应点),线段AA长度的最小值称为线段AB 到⊙O 的“平移距离”. (1)如图,平移线段AB 到⊙O 的长度为1 的弦12PP 和34P P ,则这两条弦的位置关系是 ;在点1234,,,P P P P 中,连接点A 与点 的线段的长度等于线段AB 到⊙O 的“平移距离”; 2 / 63 (2)若点A,B 都在直线32 3yx上,记线段AB 到⊙O 的“平移距离”为1d ,求1d 的最小值; (3)若点A 的坐标为32, 2 ,记线段AB 到⊙O 的“平移距离”为2d ,直接写出2d 的取值范围. 3.在△ABC 中,D ,E 分别是ABC 两边的中点,如果 DE 上的所有点都在△ABC 的内部或边上,则称 DE 为△ABC 的中内弧.例如,下图中 DE 是△ABC 的一条中内弧. (1)如图,在Rt△ABC 中,2 2ABACDE,,分别是 AB AC,的中点.画出△ABC 的最长的中内弧DE ,并直接写出此时 DE 的长; (2)在平面直角坐标系中,已知点0,20,04 ,00ABCtt ,,,在△ABC 中,D E,分别是 AB AC,的中点. ①若12t ,求△ABC 的中内弧 DE 所在圆的圆心 P 的纵坐标的取值范围; ②若在△ABC 中存在一条中内弧 DE ,使得 DE 所在圆的圆心 P 在△ABC 的内部或边上,直接写出 t的取值范围. 3 / 63 4.对于平面直角坐标系x Oy 中的图形M ,N ,给出如下定义:P 为图形M 上任意一点,Q 为图形N 上任意一点,如果P...