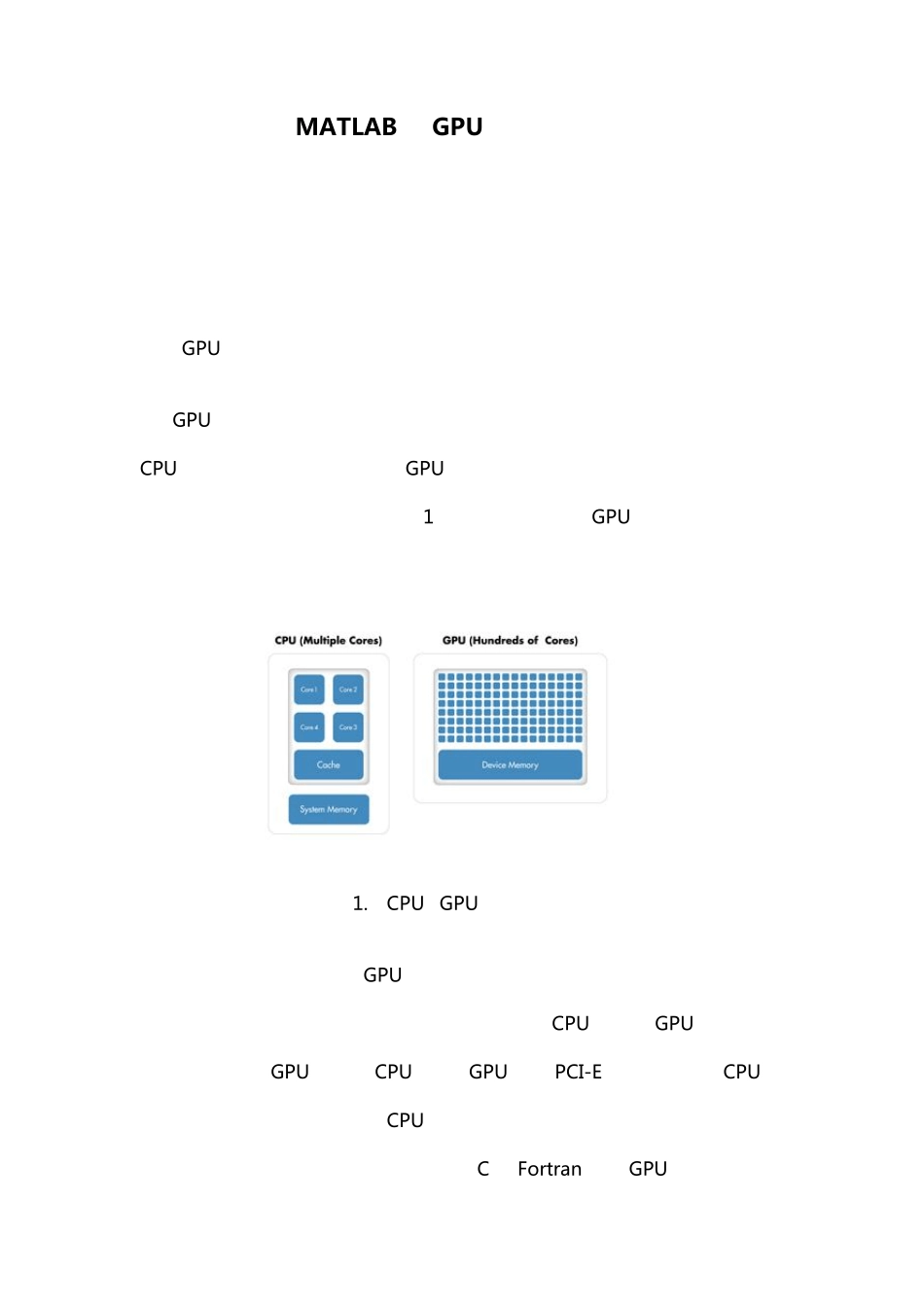
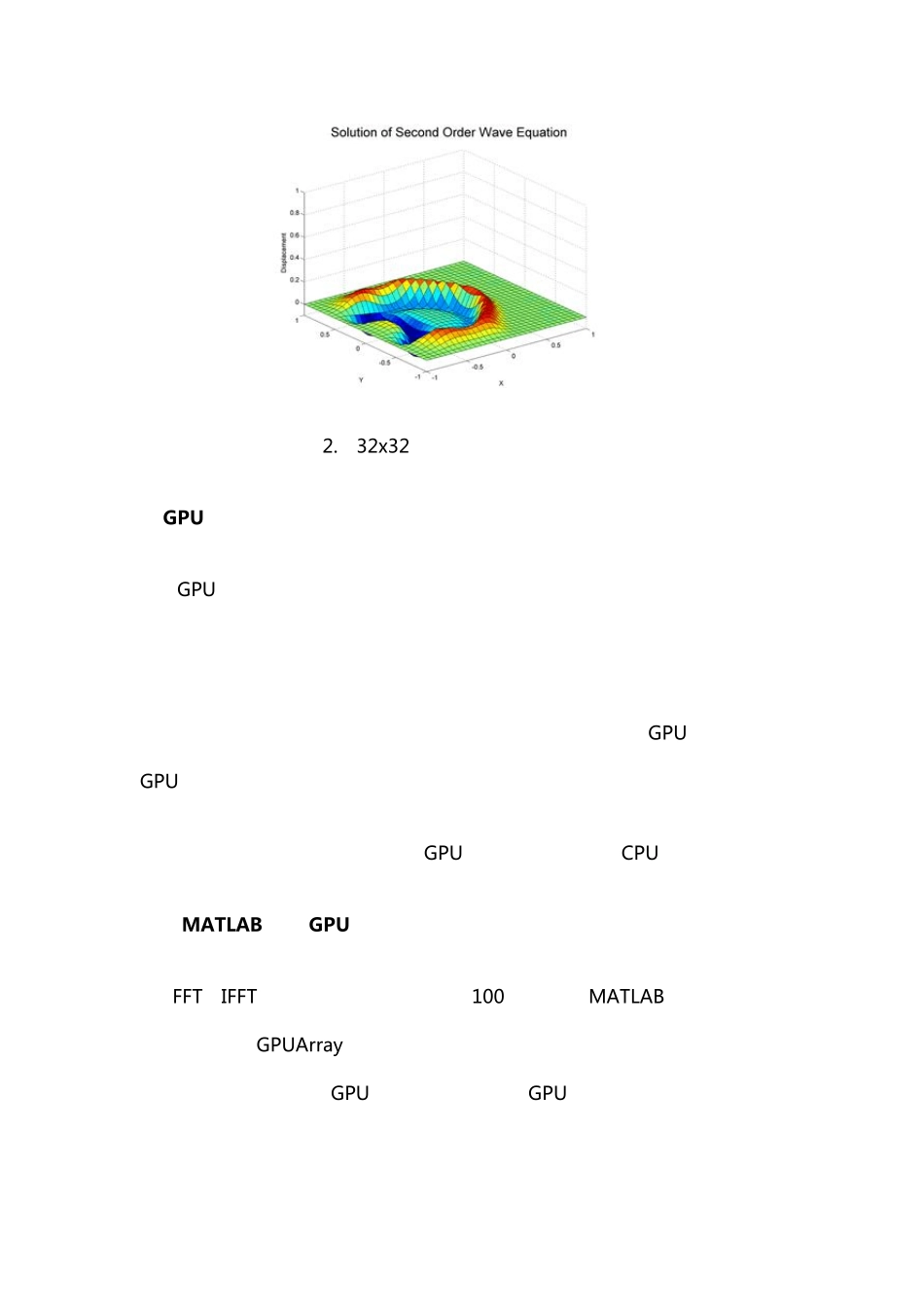
MATLAB 与 GPU 编程结合应用 多核服务器以及多线程技术使科学家,工程师以及财务分析师能够加快处理多个学科内的计算密集型应用。现在,另一种硬件承诺提供更高的计算性能,那就是 GPU。 GPU 最初用于加速图形渲染,现在越来越多地应用于科学计算。和传统的CPU 只包括少数的几个核不同,GPU 由整型和浮点处理器组成的大规模并行矩阵以及专用的高速内存构成。如图 1 所示,一个典型的 GPU 包含数百个小型处理器。 图 1. CPU和 GPU 的核心数对比 上述配置极大地增加了 GPU 的吞吐量,但同时也要付出代价。首先,内存访问很有可能会出现瓶颈。进行计算前数据必须从 CPU 发送到 GPU,计算完成后,数据必须从 GPU 发送到 CPU。因为 GPU 通过 PCI-E 总线与主机的 CPU 连接,但是内存访问要比传统的 CPU 慢很多。这意味着整体的计算加速受限于算法中用到的数据转换器数目。其次,采用 C 或 Fortran 进行 GPU 编程需要不同 的心智模型和技能,这很困难而且需要很长的时间才能达到。此外,针对特定的GPU 你必须花费时间调整代码以优化应用性能。 本文演示了并行计算工具箱的功能特性,只需要对 MATLAB 代码进行简单的修改就能够在 GPU 上运行。我们通过使用波谱法解二阶波动方程对该方法进行了举例说明。 为什么要并行化波动方程求解程序? 波动方程广泛用于工程专业包括地震学,流体动力学,声学,以及电磁学,用于描述声,光和流体波。 使用波谱法解波动方程的算法能够实现并行是因为它满足使用 GPU 进行加速的两个标准: 大规模并行。并行快速傅里叶变化(FFT)算法的目的在于“分而治之”,这样一个相似的任务能够采用不同的数据反复执行。此外,该算法要求在处理线程和大量的内存带宽之间进行大量的通信。反向快速傅里叶变换(IFFT)同样能够并行运行。 计算密集型。算法执行大量的 FFT 以及 IFFT,准确的数字取决于网格的规模和仿真中时间步长的数量。每个时间步长需要两个 FFT,四个 IFFT,而单个计算可能包含成千上万的时间步长。 图 2. 32x32网格矩阵波动方程解决方案 在 GPU 上执行能够加快我的应用程序吗? GPU 能够对符合以下标准的应用程序进行加速: 大规模并行—计算能够被分割成上百个或上千个独立的工作单元。 计算密集型—计算消耗的时间显著超过了花费转移数据到 GPU 内存以及从GPU 内存转移出数据的时间。 不满足上述标准的应用程序在 GPU 上运行时可能会...