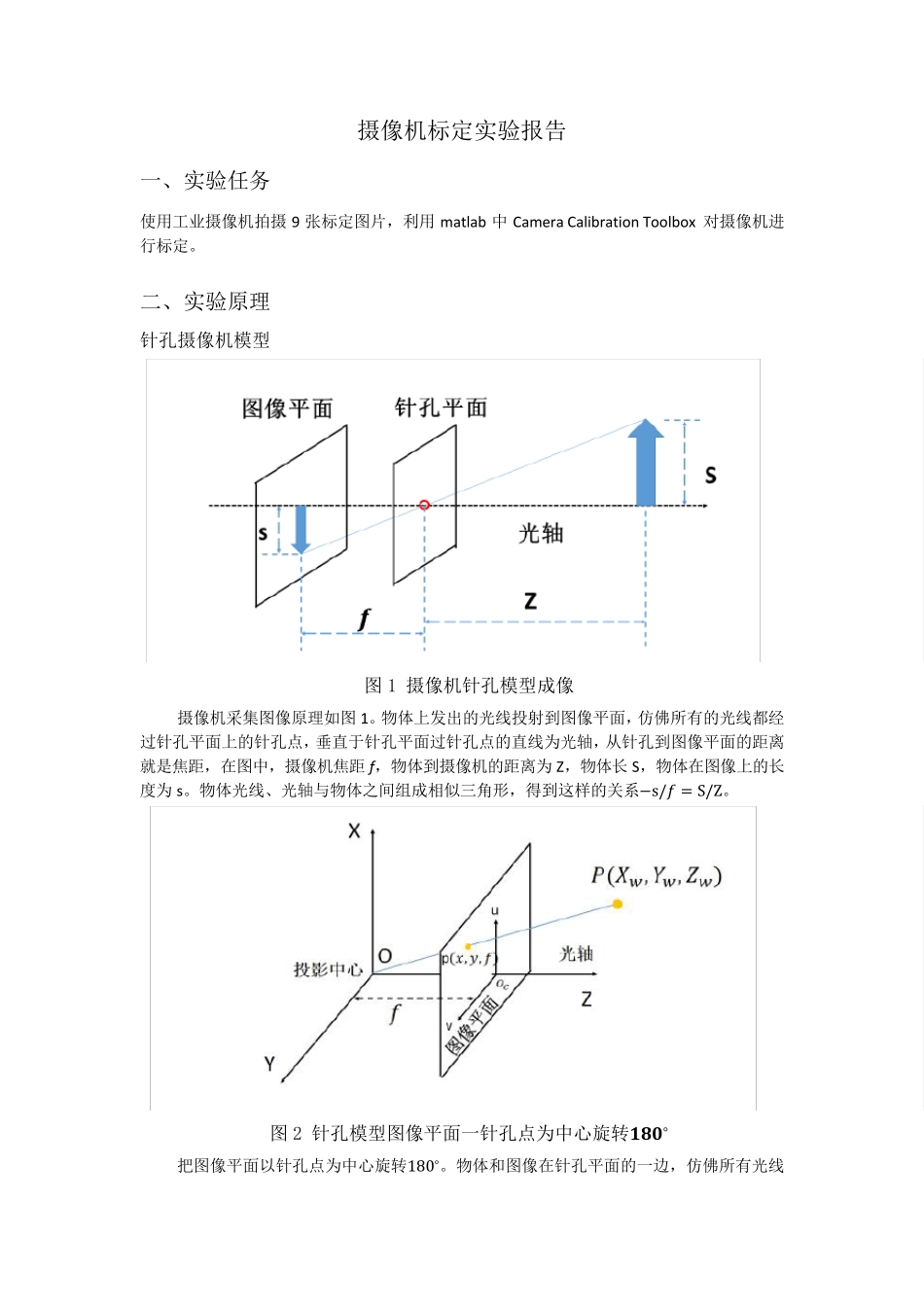
摄像机标定实验报告 一、实验任务 使用工业摄像机拍摄9 张标定图片,利用 matlab 中 Camera Calibration Toolbox 对摄像机进行标定。 二、实验原理 针孔摄像机模型 图 1 摄像机针孔模型成像 摄像机采集图像原理如图 1。物体上发出的光线投射到图像平面,仿佛所有的光线都经过针孔平面上的针孔点,垂直于针孔平面过针孔点的直线为光轴,从针孔到图像平面的距离就是焦距,在图中,摄像机焦距 f ,物体到摄像机的距离为 Z,物体长 S,物体在图像上的长度为 s。物体光线、光轴与物体之间组成相似三角形,得到这样的关系−s/ᵅ = S/Z。 图 2 针孔模型图像平面一针孔点为中心旋转ᵼ ᵽ ᵼ° 把图像平面以针孔点为中心旋转180°。物体和图像在针孔平面的一边,仿佛所有光线从物体走到图像平面成像的对应点,最后汇集到一点,这个点定义为投影中心[33]。图3-22中点O 为投影中心。 在抽象的针孔模型中点P(ᵄᵆ,ᵄᵆ, ᵄᵆ)由通过投影中心O 的光线投影到图像平面上,相应的图像点为p(x, y, ᵅ)。成像芯片的中心通常不在光轴上,定义图像平面与光轴交点为主点ᵅᵅ坐标(ᵅᵆ, ᵅᵆ)。ᵅ为透镜的物理焦距,定义ᵅᵆ为焦距长度与像素x 轴方向长度的比,定义ᵅᵆ为焦距长度与像素y 轴方向长度的比。可以得到 x = ᵅᵆ (ᵄᵆᵄᵆ) + ᵅᵆ (1) ᵆ = ᵅᵆ ( ᵄᵆᵄᵆ) + ᵅᵆ (2) 将坐标为(X, Y, Z)的物理点映射到投影平面上坐标为(x,y)的过程叫投影变换。齐次坐标可以建立这种变换。齐次坐标把维数为n 投影空间的点表示成(n+1)维向量。图像平面为二维投影空间,可用三维向量表示该平面上的点。将摄像机参数ᵅᵆ、ᵅᵆ、ᵅᵆ、ᵅᵆ重新排列为一个3×3 的矩阵,如 M,该矩阵就是摄像机内部参数矩阵。将物理世界中的点投射到摄像机上,用下式表示: p = MP,其中p = [ᵆᵆᵆ] ,M = [ᵅᵆ0ᵅᵆ0ᵅᵆᵅᵆ001] ,P = [ᵄᵆᵄᵆᵄᵆ] (3) 标定过程 摄像机参数ᵅᵆ、ᵅᵆ、ᵅᵆ、ᵅᵆ、倾斜系数需要通过计算得到,这一过程为摄像机标定。标定过程就是确定摄像机的几何和光学参数、摄像机相对于世界坐标系的。 三、实验步骤与结果 本实验使用Matlab 中Camera Calibration Toolbox 对摄像机进行标定。 首先,于 2014 年 3 月 1 日下午在科研一楼 503 实验室拍摄一组 9 张平面棋盘图片,如图。 接着,连接在http://www.vision.caltech.edu/bouguetj/calib_doc/download/index.h...