MATLAB线性系统时域响应分析实验VIP免费

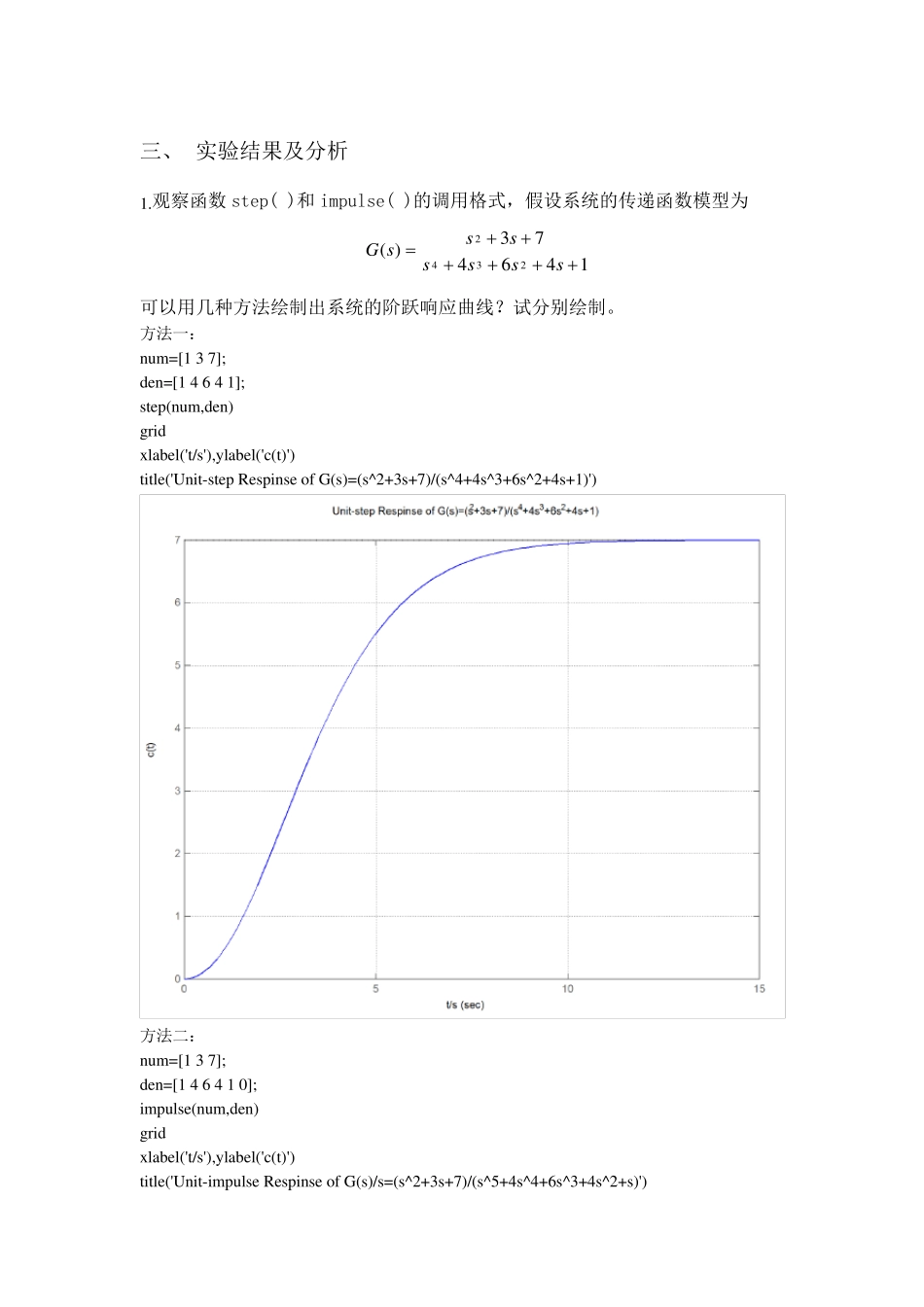
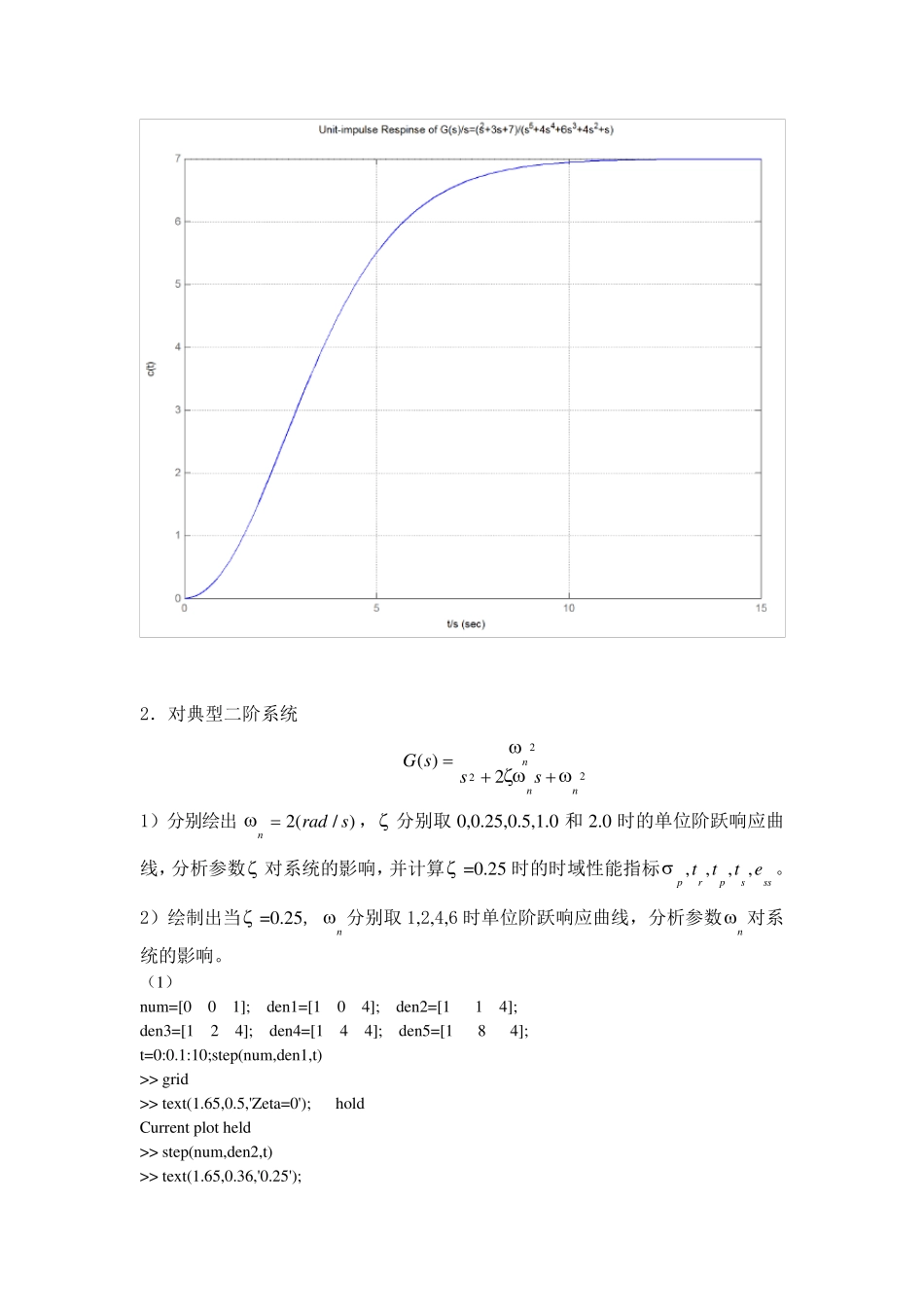
实验报告 实验名称 线性系统时域响应分析 一、 实验目的 1．熟练掌握 step( )函数和 impulse( )函数的使用方法，研究线性系统在单位阶跃、单位脉冲及单位斜坡函数作用下的响应。 2．通过响应曲线观测特征参量 和n 对二阶系统性能的影响。 3．熟练掌握系统的稳定性的判断方法。 二、 实验内容 1．观察函数 step( )和 impulse( )的调用格式，假设系统的传递函数模型为 146473)(2342sssssssG 可以用几种方法绘制出系统的阶跃响应曲线？试分别绘制。 2．对典型二阶系统 2222)(nnnsssG 1）分别绘出)/(2sradn ， 分别取 0,0.25,0.5,1.0 和 2.0 时的单位阶跃响应曲线，分析参数  对系统的影响，并计算  =0.25 时的时域性能指标sssprpettt,,,,。 2）绘制出当 =0.25, n 分别取 1,2,4,6 时单位阶跃响应曲线，分析参数n对系统的影响。 3．系统的特征方程式为010532234ssss，试用两种判稳方式判别该系统的稳定性。 4．单位负反馈系统的开环模型为 )256)(4)(2()(2ssssKsG 试用劳斯稳定判据判断系统的稳定性，并求出使得闭环系统稳定的K 值范围。 三、 实验结果及分析 1.观察函数 step( )和 impulse( )的调用格式，假设系统的传递函数模型为 146473)(2342sssssssG 可以用几种方法绘制出系统的阶跃响应曲线？试分别绘制。 方法一： nu m=[1 3 7]; den=[1 4 6 4 1]; step(nu m,den) grid x label('t/s'),y label('c(t)') title('Unit-step Respinse of G(s)=(s^2+3s+7)/(s^4+4s^3+6s^2+4s+1)') 方法二： nu m=[1 3 7]; den=[1 4 6 4 1 0]; impu lse(nu m,den) grid x label('t/s'),y label('c(t)') title('Unit-impu lse Respinse of G(s)/s=(s^2+3s+7)/(s^5+4s^4+6s^3+4s^2+s)') 2．对典型二阶系统 2222)(nnnsssG 1）分别绘出)/(2sradn ， 分别取0,0.25,0.5,1.0 和2.0 时的单位阶跃响应曲线，分析参数 对系统的影响，并计算 =0.25 时的时域性能指标sssprpettt,,,,。 2）绘制出当 =0.25, n 分别取1,2,4,6 时单位阶跃响应曲线，分析参数n 对系统的影响。 （1） nu m=[0 0 1]; den1=[1 0 4]; den2=[1 1 4]; den3=[1 2 4]; den4=[1 4 4]; den5=[1 8 4]; t=0:0.1:10;step(nu m,den1,t) >> grid ...