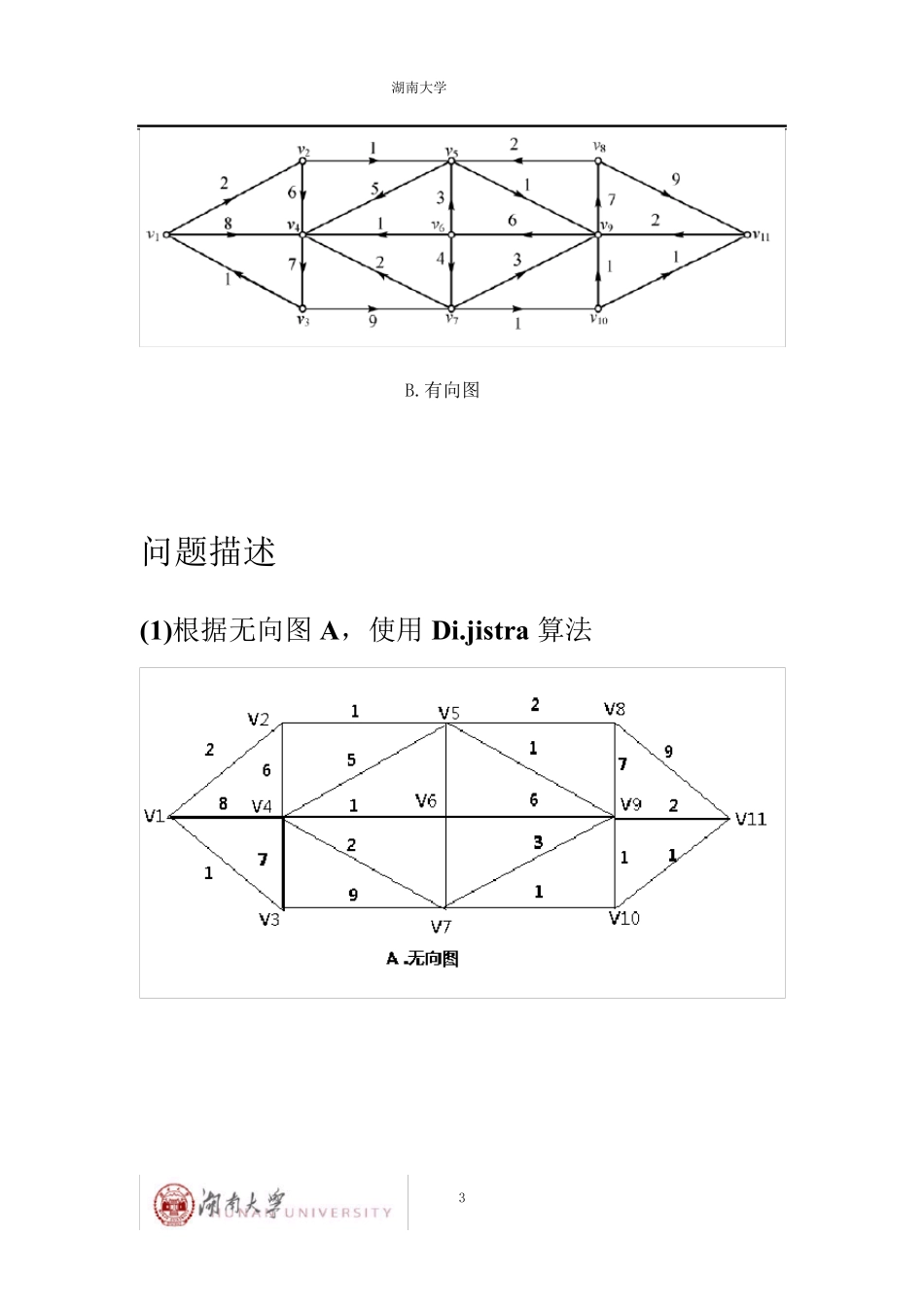
湖南大学 1 湖南大学 MATLAB 实训报告 题 目: matlab 计算最短路径问题 学院名称:信息科学与工程学院 专业班级: 软件工程四班 学生姓名: *** 学 号: *********** 日 期: 2013 年 7 月 3 号 湖南大学 2 目录 题目 .............................................................. 2 问题描述 .......................................................... 3 (1) 根据无向图A,使用Di.jistra 算法.......................... 3 (2)根据有向图B,使用Warshall-Floyd算法 ...................... 4 思路及代码 ........................................................ 4 (1)思路....................................................... 4 (2)源代码..................................................... 5 测试结果说明 ..................................................... 10 (1)Di.jistra算法 .............................................. 10 (2)Floyd 算法 .................................................. 11 小结 ............................................................. 11 题目 求下图中顶点ν1到顶点ν11的最短距离和最短路(2学分) 湖南大学 3 B.有向图 问题描述 (1)根据无向图A,使用 Di.jistra 算法 湖南大学 4 (2)根据有向图B,使用Warshall-Floyd 算法 思路及代码 (1)思路 (1)Dijkstra 算法 使用范围: 1) 寻求从一固定顶点到其余各点的最短路径; 2) 有向图、无向图和混合图; 3) 权非负. 算法思路: 采用标号作业法,每次迭代产生一个永久标号, 从而生长一颗以 v0为根的最短路树,在这颗树上每个顶点与根节点之间的路径皆为最短路径. 诉法步骤: S: 具有永久标号的顶点集; l(v): v 的标记; f(v):v 的父顶点,用以确定最短路径; 输入加权图的带权邻接矩阵 w=[w(vi,vj)]nxm. 1) 初始化 令 l(v0)=0,S=; vv0 ,l(v)=; 2) 更新 l(v), f(v) 寻找不在 S 中的顶点u,使l(u)为最小.把 u 加入到S 中,然后对所有不在S中 的顶点v, 如l(v)>l(u)+w(u,v), 则 更 新l(v),f(v), 即 l(v) l(u)+w(u,v),f(v) u; 3) 重复步骤 2), 直到所有顶点都在 S 中为止. (2)Floyd 算法 使用范围: 1) 求每对顶点的最短路径; 2) 有向图、无向图和混合图; 湖南大学 5 算...