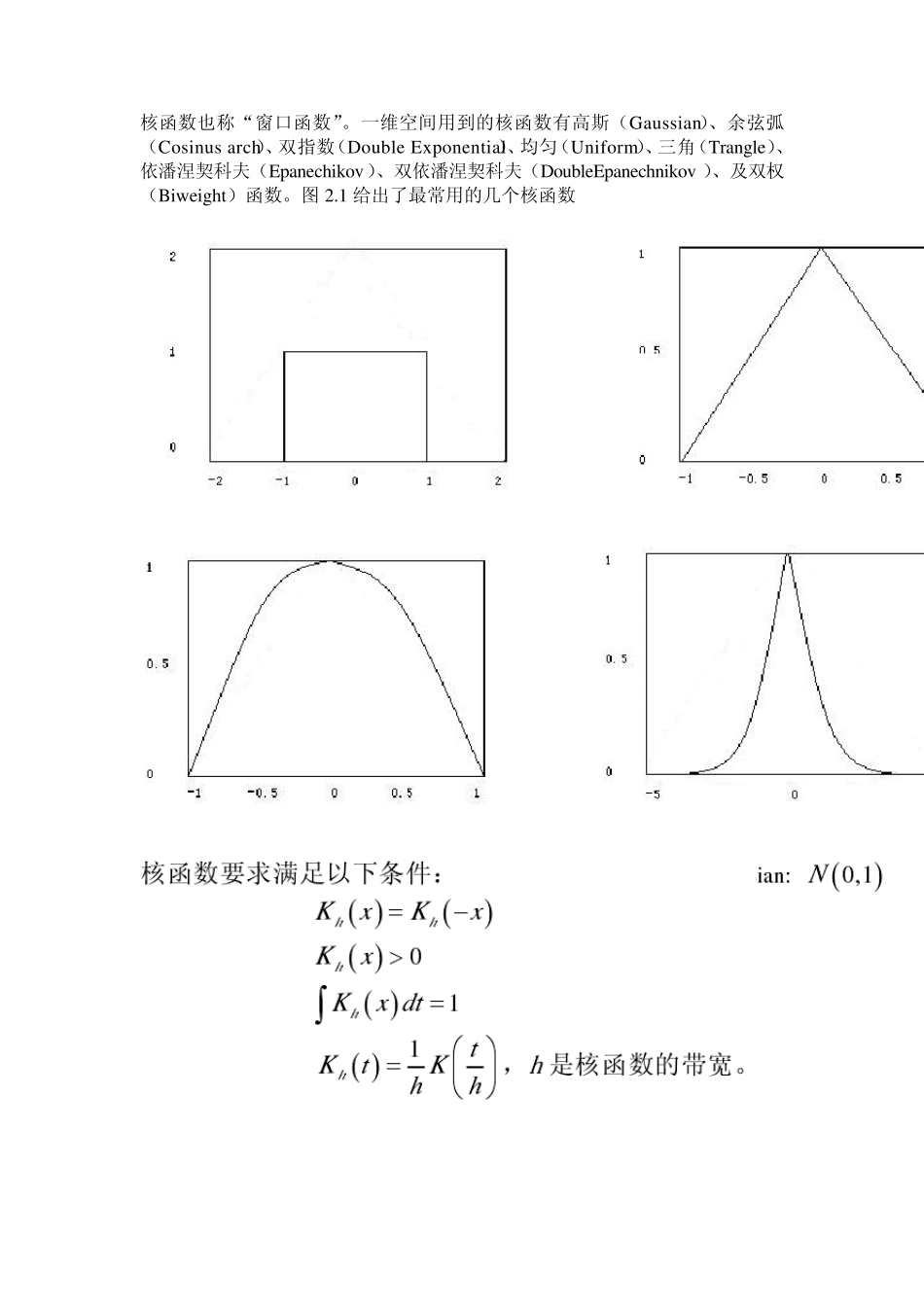
核函数也称“窗口函数”。一维空间用到的核函数有高斯(Gaussian)、余弦弧(Cosinus arch)、双指数(Double Exponential)、均匀(Uniform)、三角(Trangle)、依潘涅契科夫(Epanechikov)、双依潘涅契科夫(DoubleEpanechnikov )、及双权(Biweight)函数。图 2.1 给出了最常用的几个核函数 给定一组一维空间的n 个数据点集合令该数据集合的概率密度函数假设为f (x ),核函数取值为,那么在数据点x 处的密度估计可以按下式计算: 上式就是核密度估计的定义。其中,x 为核函数要处理的数据的中心点,即数据集合相对于点x 几何图形对称。核密度估计的含义可以理解为:核估计器在被估计点为中心的窗口内计算数据点加权的局部平均。或者:将在每个采样点为中心的局部函数的平均效果作为该采样点概率密度函数的估计值。 MeanShift实现: 1.选择窗的大小和初始位置. 2.计算此时窗口内的Mass Center. 3.调整窗口的中心到Mass Center. 4.重复2 和3,直到窗口中心"会聚",即每次窗口移动的距离小于一定的阈值,或者迭代次数达到设定值。 meanshift 算法思想其实很简单:利用概率密度的梯度爬升来寻找局部最优。它要做的就是输入一个在图像的范围,然后一直迭代(朝着重心迭代)直到满足你的要求为止。但是他是怎么用于做图像跟踪的呢?这是我自从学习 meanshift 以来,一直的困惑。而且网上也没有合理的解释。经过这几天的思考,和对反向投影的理解使得我对它的原理有了大致的认识。 在 opencv 中,进行 meanshift 其实很简单,输入一张图像(imgProb),再输入一个开始迭代的方框(w indow In)和一个迭代条件(criteria),输出的是迭代完成的位置(comp )。 这是函数原型: int cvMeanShift( const void* imgProb, CvRect w indow In,CvTermCriteria criteria, CvConnectedComp* comp ) 但是当它用于跟踪时,这张输入的图像就必须是反向投影图了。 为什么必须是反向投影图呢?首先我们要理解什么是反向投影图。 简单理解它其实实际上是一张概率密度图。经过反向投影时的输入是一个目标图像的直方图(也可以认为是目标图像),还一个输入是当前图像就是你要跟踪的全图,输出大小与全图一样大,它上像素点表征着一种概率,就是全图上这个点是目标图像一部分的概率。如果这个点越亮,就说明这个点属于物体的概率越大。现在我们明白了这原来是一张概率图了。当用 meanshift 跟踪时,输入的原来是...