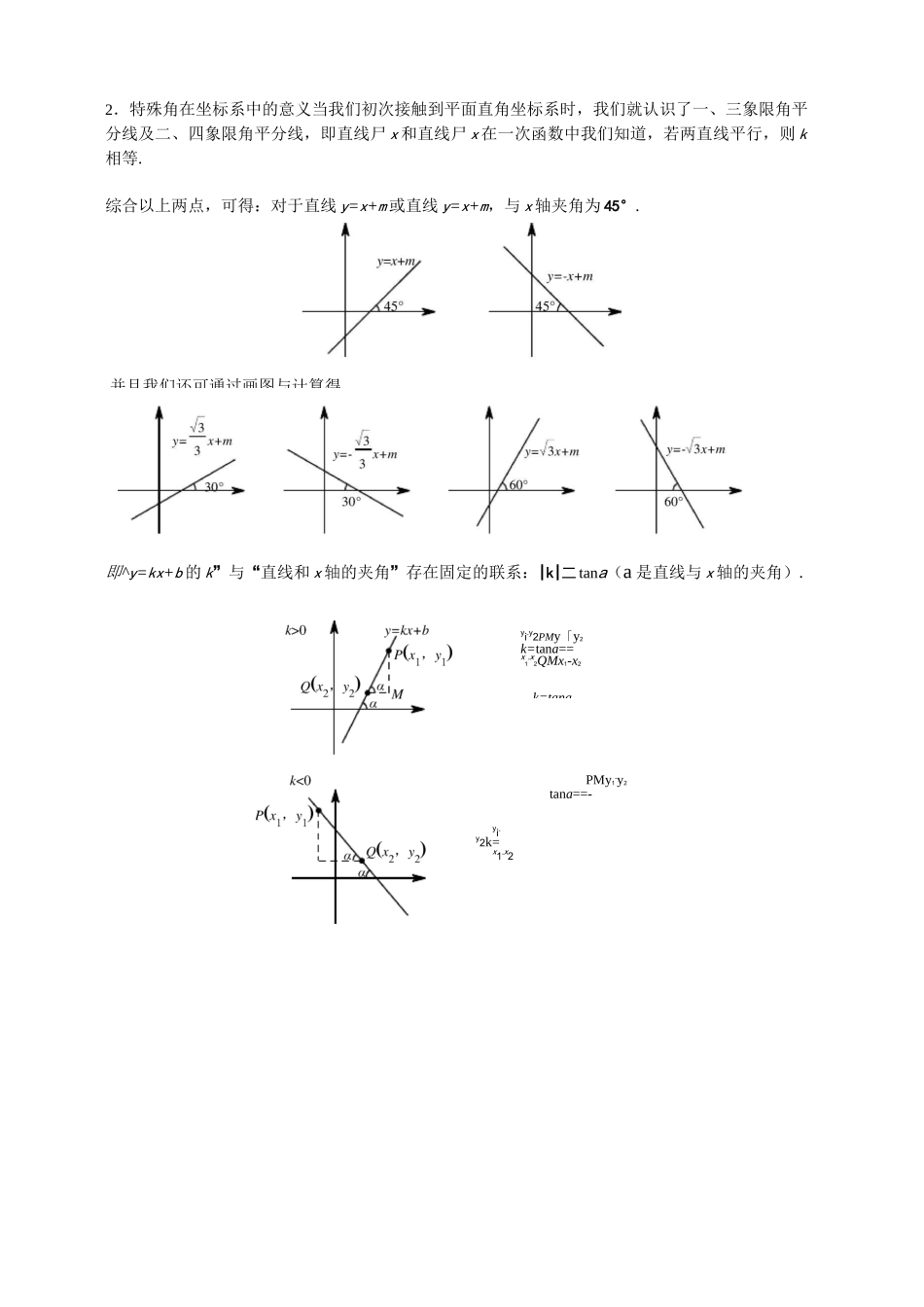
二次函数中的特殊角问题Section1 特殊角的认识知识总结1.什么是特殊角?说到特殊角我们很快就能想到比如 30。、45。、60。、90°等,事实上,之所以以上角能称为特殊角,关键在于这些角的三角函数值特殊,比如为什么我们会将 60。称为特殊角,而 50。便不是,原因很简单,1cos60o=,而我们并不知道 50°的任一三角函数值.2因此角度特殊不在于这个角是多少度,而在于其三角函数值是否有特殊值,所以除了常见的 30。、45。、60°,我们可以扩充一下特殊角的范围.三边之比为 1:3:2三边之比为 1:三边之比为 1:3:2三边之比为 1:2:51tana=""23tan®+45°)=21三边之比为 1:tan(a+45°)=3k=tana2.特殊角在坐标系中的意义当我们初次接触到平面直角坐标系时,我们就认识了一、三象限角平分线及二、四象限角平分线,即直线尸 x 和直线尸 x 在一次函数中我们知道,若两直线平行,则 k相等.综合以上两点,可得:对于直线 y=x+m 或直线 y=x+m,与 x 轴夹角为 45°.即^y=kx+b 的 k”与“直线和 x 轴的夹角”存在固定的联系:|k|二 tana(a 是直线与 x 轴的夹角).yi-y2PMy「y2k=tana==x1-x2QMx1-x2PMy1-y2tana==-并且我们还可通过画图与计算得yi-y2k=x1-x2