§2.3牛顿(Newton)法及其变形VIP免费

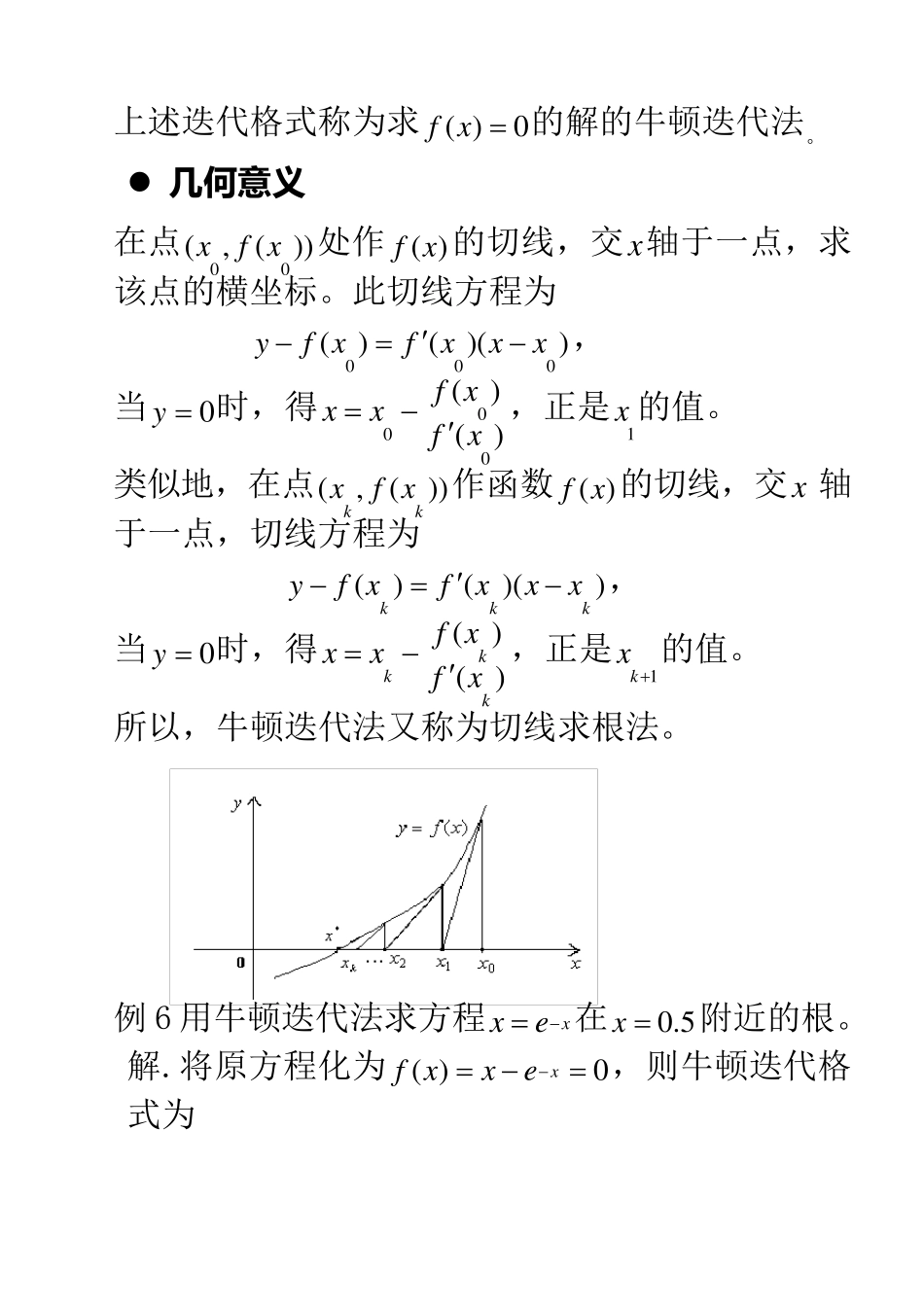
2.3 牛 顿 （ Newton） 法 及 其 变 形 一、Newton 迭代方法  牛 顿 迭 代法计算公式的推导过程 设*x 是( )0f x  的根，( )f x 在*x 的邻域内具有二阶连续导数，在*x 的邻域内取一点0x ，使0()0fx ，则( )f x 在*x 的邻域内连续，将它在0x 点二阶Taylor展开得 20000000( )( )()()()()2 !()()()ff xf xfxxxxxf xfxxx 又( )0f x  ，则有 000()()()0f xfxxx 故( )0f x  的近似解000()()f xxxfx，记0100()()f xxxfx 类似，在点1x 处 Taylor 展开，可得： 111( )( )f xxxfx，记1211( )( )f xxxfx 依次往下做，可得一般的迭代格式： 1() ,(0 ,1 ,)()kkkkf xxxkfx  上述迭代格式称为求( )0f x  的解的牛顿迭代法。  几 何 意 义 在点00(,())xf x处作( )f x 的切线，交x 轴于一点，求该点的横坐标。此切线方程为 000()()()yf xfxxx， 当0y  时，得000()()f xxxfx，正是1x 的值。 类似地，在点(,())kkxf x作函数( )f x 的切线，交 x 轴于一点，切线方程为 ()()()kkkyf xfxxx， 当0y  时，得()()kkkf xxxfx，正是1kx 的值。 所以，牛顿迭代法又称为切线求根法。 例 6 用牛顿迭代法求方程xxe在0 .5x 附近的根。 解.将原方程化为( )0xf xxe ，则牛顿迭代格式为 11kkxkkkxxexxe 取00 .5x ，迭代得 1230 .5 6 6 3 1 1 0 .5 6 7 1 4 3 1 , 0 .5 6 7 1 4 3 3xxx 与上一节例2-4 相比,牛顿法的收敛速度快。与埃特金法相当. 注意：牛顿法的几何意义说明了，迭代初值0x 必须足够接近*x ，否则可能不收敛或收敛与其它的根。 牛顿迭代法的流程图 输入迭代初始值0x ，精度 ，最大迭代次数 N Nk,,2,1 0'0 f T F 输出0'0 f的信息，结束 000'/ ffxx 1x T F 0xxE xxxE/0 E T F 输出kxfx),(,，结束 xx0 输出迭代N 次失败信息，停。 )(''),(0000xffxff二、Newton 迭代法的变形 牛顿法的优 点 :收敛速度快。 牛顿法的缺 点 :每次迭代要计算一次导数值'()kfx，当 ( )f x 表达式复杂或无明显表达式时求解困难。  简 化 的 牛 顿 迭 代法 1.主 要 思 路 :为了...