《数值分析》上机实验报告VIP免费

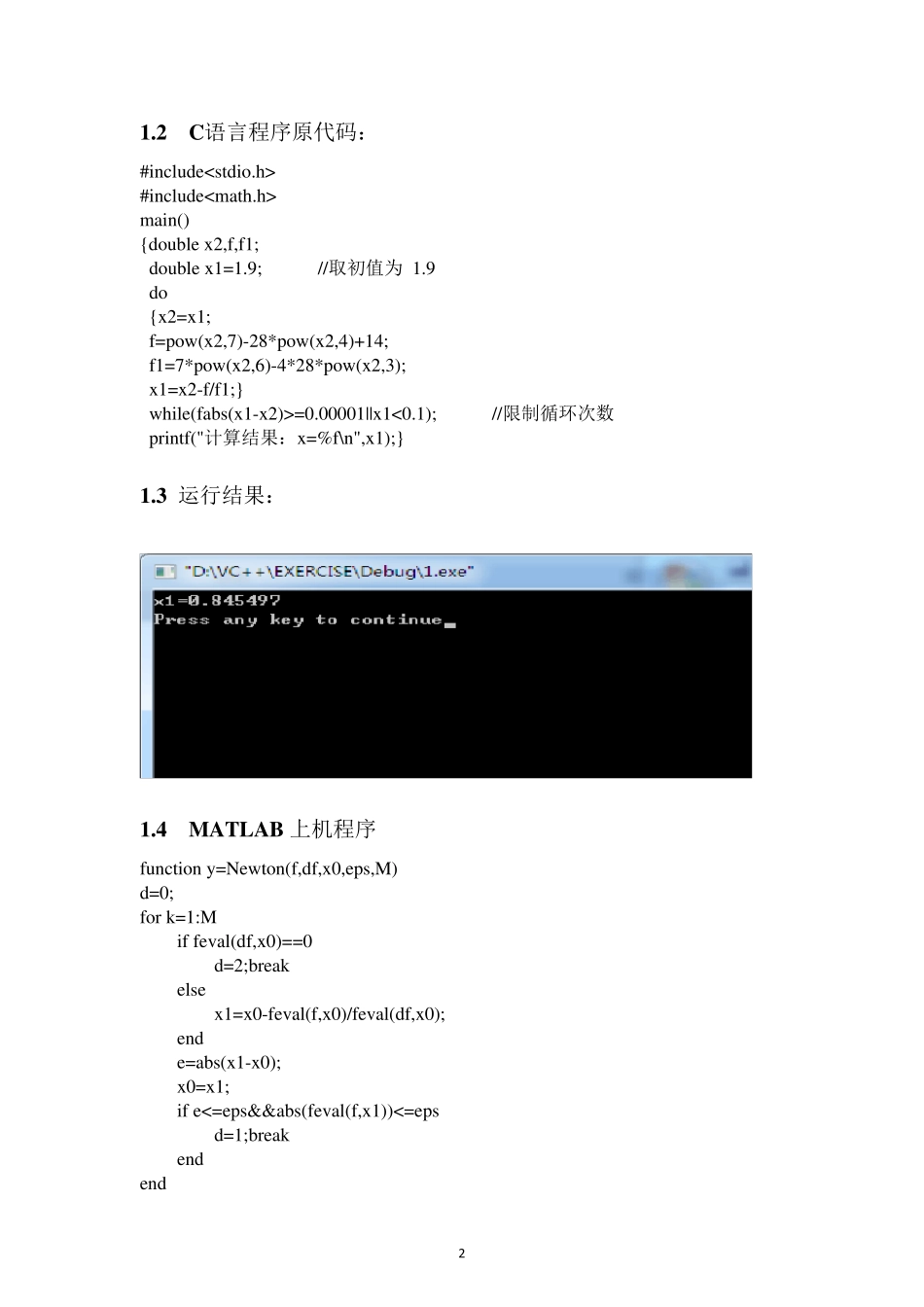
数值分析上机实验报告 1 《数值分析》上机实验报告 1 .用Newton 法求方程 X7-X4+14=0 在（0.1，1.9）中的近似根（初始近似值取为区间端点，迭代6 次或误差小于0.00001）。 1 .1 理论依据： 设函数在有限区间[a，b]上二阶导数存在，且满足条件  上的惟一解在区间平方收敛于方程所生的迭代序列迭代过程由则对任意初始近似值达到的一个中使是其中上不变号在区间],[0)(3,2,1,0,)(')()(],,[x|))(),((|,|,)(||)(|.4;0)(.3],[)(.20)()(.110......baxfxkxfxfxxxNewtonbabfafmirbacxfabcfxfbaxfbfxfkkkkkk 令 0)9.1()9.1(0)8(4233642)(0)16(71127)(0)9.1(,0)1.0(,1428)(3225333647ffxxxxxfxxxxxfffxxxf 故以 1.9 为起点 9.1)()(01xxfxfxxkkkk 如此一次一次的迭代，逼近x的真实根。当前后两个的差<=ε时，就认为求出了近似的根。本程序用Newton法求代数方程(最高次数不大于10)在（a,b）区间的根。 2 1.2 C语言程序原代码： #include #include main() {double x2,f,f1; double x1=1.9; //取初值为 1.9 do {x2=x1; f=pow(x2,7)-28*pow(x2,4)+14; f1=7*pow(x2,6)-4*28*pow(x2,3); x1=x2-f/f1;} while(fabs(x1-x2)>=0.00001||x1<0.1); //限制循环次数 printf("计算结果：x=%f\n",x1);} 1.3 运行结果： 1.4 MATLAB 上机程序 function y=Newton(f,df,x0,eps,M) d=0; for k=1:M if feval(df,x0)==0 d=2;break else x1=x0-feval(f,x0)/feval(df,x0); end e=abs(x1-x0); x0=x1; if e<=eps&&abs(feval(f,x1))<=eps d=1;break end end 3 if d==1 y=x1; elseif d==0 y='迭代M 次失败'; else y= '奇异' end function y=df(x) y=7*x^6-28*4*x^3; End function y=f(x) y=x^7-28*x^4+14; End >> x0=1.9; >> eps=0.00001; >> M=100; >> x=Newton('f','df',x0,eps,M); >> vpa(x,7) 1.5 问题讨论： 1.使用此方法求方解，用误差来控制循环迭代次数，可以在误差允许的范围内得到比较理想的计算结果。此程序的不足之处是，所要求解的方程必须满足上述定理的四个条件，但是第二和第四个条件在计算机上比较难以实现。 2.Newton 迭代法是一个二阶收敛迭代式，他的几何意义 Xi+1 是 Xi 的切线与x 轴的交点,故也称为切线法。它是平方收敛的，但它是局部...