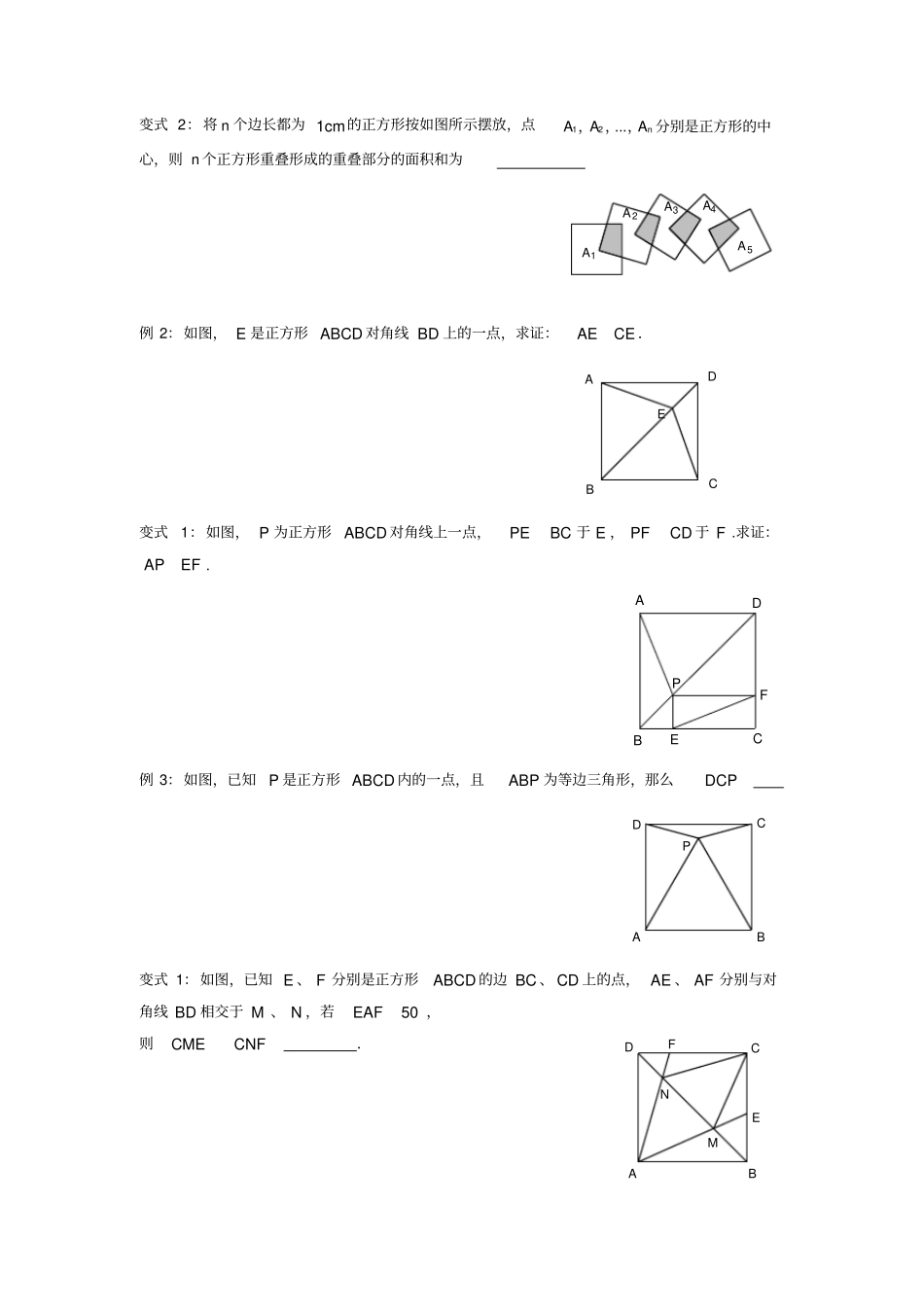
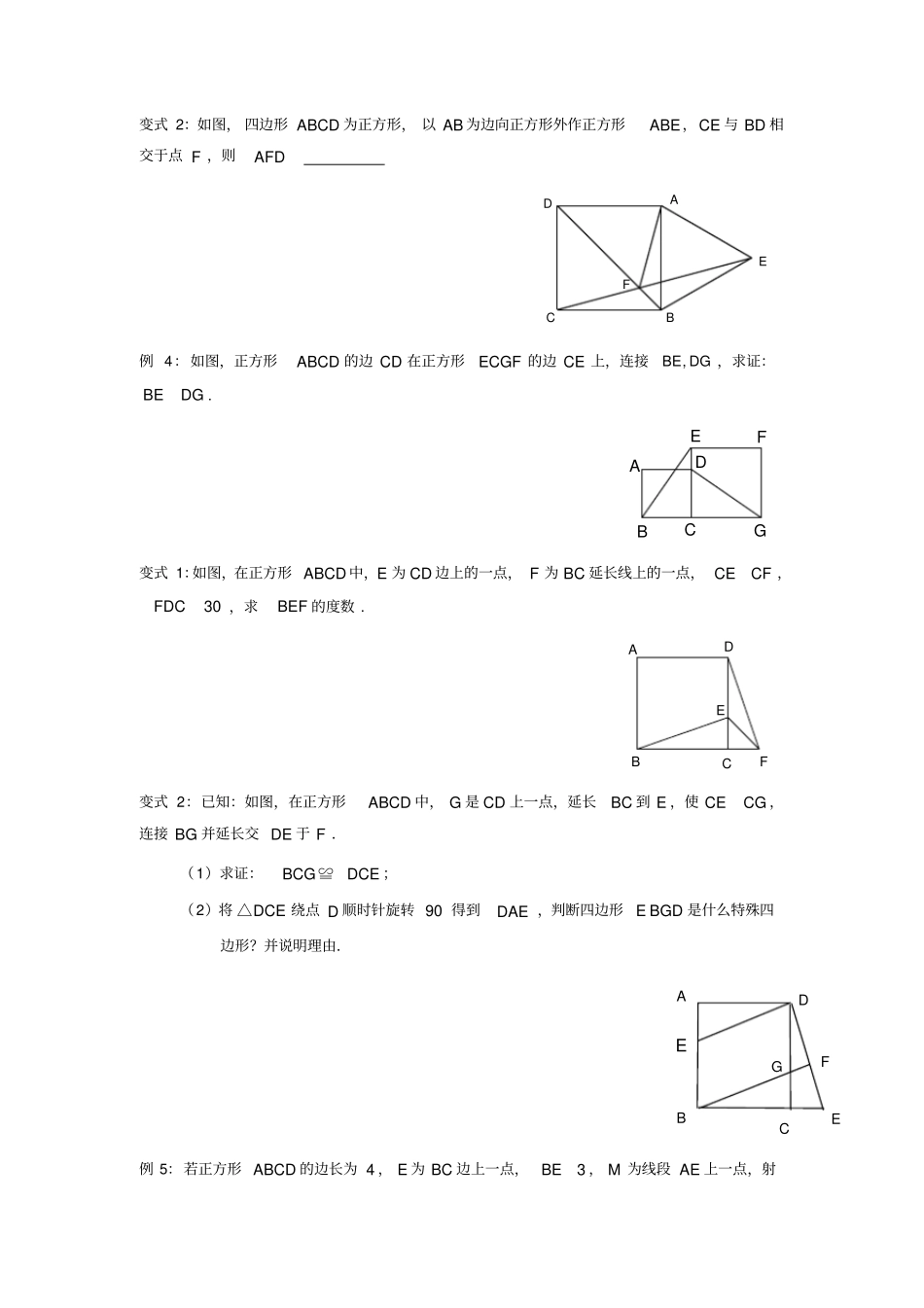
正方形的性质及判定知识归纳1.正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.2.正方形的性质正方形是特殊的平行四边形、矩形、菱形.它具有前三者的所有性质:① 边的性质:对边平行,四条边都相等.② 角的性质:四个角都是直角.③ 对角线性质:两条对角线互相垂直平分且相等,每条对角线平分一组对角.④ 对称性:正方形是中心对称图形,也是轴对称图形.平行四边形、矩形、菱形和正方形的关系:(如图)3.正方形的判定判定①:有一组邻边相等的矩形是正方形.判定②:有一个角是直角的菱形是正方形.4.重点:知晓正方形的性质和正方形的判定方法。难点:正方形知识的灵活应用例题讲解一、正方形的性质例 1:如图,已知正方形ABCD 的面积为 256 ,点 F 在 CD 上,点 E 在 CB 的延长线上,且20AEAFAF,,则 BE 的长为FEDCBA变式 1:如图,在正方形ABCD 中, E 为 AB 边的中点, G , F 分别为 AD , BC 边上的点,若1AG,2BF,90GEF,则 GF 的长为.正方形菱形矩形平行四边形变式 2:将 n 个边长都为 1cm的正方形按如图所示摆放,点12 ...nAAA,, ,分别是正方形的中心,则 n 个正方形重叠形成的重叠部分的面积和为A5A4A3A2A1例 2:如图, E 是正方形 ABCD 对角线 BD 上的一点,求证:AECE .EDCBA变式1:如图, P 为正方形ABCD 对角线上一点,PEBC 于 E , PFCD 于 F .求证:APEF . FEPDCBA例 3:如图,已知P 是正方形 ABCD 内的一点,且ABP 为等边三角形,那么DCPPDCBA变式 1:如图,已知 E 、 F 分别是正方形ABCD 的边 BC 、 CD 上的点, AE 、 AF 分别与对角线 BD 相交于 M 、 N ,若50EAF,则CMECNF.NMFEDCBA变式 2:如图, 四边形 ABCD 为正方形, 以 AB 为边向正方形外作正方形ABE,CE 与 BD 相交于点 F ,则AFDFEDCBA例 4:如图,正方形ABCD 的边 CD 在正方形ECGF 的边 CE 上,连接,BE DG ,求证:BEDG . GCFEDBA变式 1:如图,在正方形 ABCD 中,E 为 CD 边上的一点, F 为 BC 延长线上的一点, CECF ,30FDC,求BEF 的度数 . BDCAEF变式 2:已知:如图,在正方形ABCD 中, G 是 CD 上一点,延长BC 到 E ,使 CECG ,连接 BG 并延长交 DE 于 F .(1)求证:BCGDCE≌;(2)将DCE△绕点 D 顺时针旋转 90 得到DAE ,判断四边形E BGD 是什么...