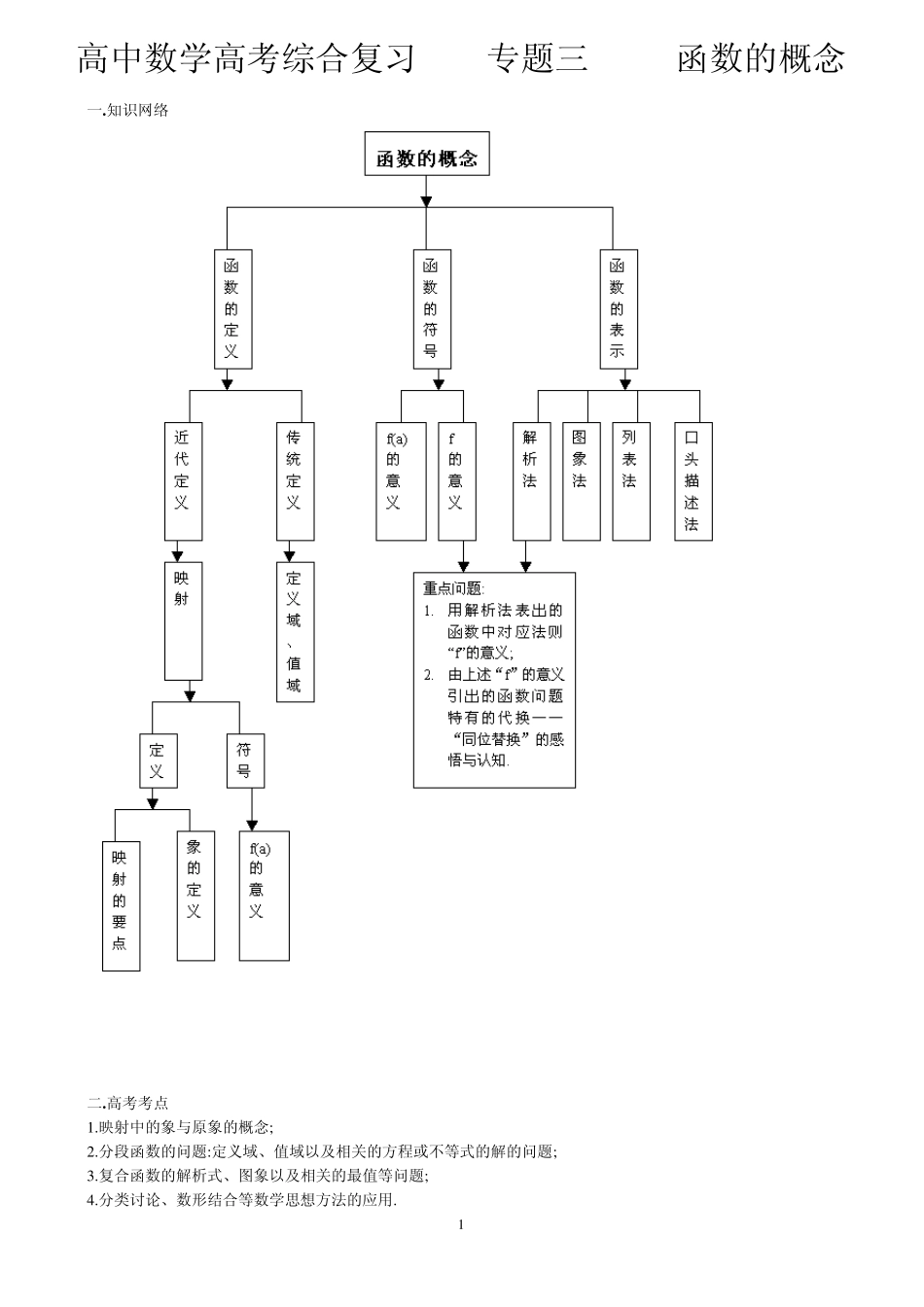
1 高中数学高考综合复习 专题三 函数的概念 一.知识网络 二.高考考点 1.映射中的象与原象的概念; 2.分段函数的问题:定义域、值域以及相关的方程或不等式的解的问题; 3.复合函数的解析式、图象以及相关的最值等问题; 4.分类讨论、数形结合等数学思想方法的应用. 2 三.知识要点 (一)函数的定义 1、传统定义:设在某一变化过程中有两个变量x 和y,如果对于某一范围内x 的每一个值,y 都有唯一的值和它对应,那么就说y 是x 的函数,x 叫做自变量,y 叫做因变量(函数). 2、现代定义:设A、B 是两个非空数集,如果按照某个确定的对应关系f,使对于集合A 中的任意一个数x ,在集合B 中都有唯一确定的数f(x)和它对应,那么就称 f:A→B 为从集合A 到集合B 的一个函数,记作y=f(x),x∈A.其中,x 叫做自变量,x的取值范围A 叫做函数的定义域;与 x 的值相对应的y 的值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域. 3、认知: ①注意到现代定义中“A、B 是非空数集”,因此,今后若求得函数定义域或值域为φ,则此函数不存在. ②函数对应关系、定义域和值域是函数的三要素,缺一不可.在函数的三要素中,对应关系是核心,定义域是基础,当函数的定义域和对应法则确定之后,其值域也随之确定. (二).映射的概念 将函数定义中的两个集合从非空数集扩展到任意元素的集合,便得到映射概念. 1、定义1:设A、B 是两个集合,如果按照某种对应法则 f,对于集合A 中任何一个元素,在集合B 中都有唯一的元素和它对应,那么这样的对应(包括集合A、B 及集合A 到集合B 的对应法则 f)叫做集合A 到集合B 的映射,记作 f:A→B 2、定义2:给定一个集合A 到集合B 的映射 f:A→B,且 a∈A,b∈B,如果在此映射之下元素 a 和元素 b 对应,则将元素b 叫做元素 a 的象,元素 a 叫做元素 b 的原象.即如果在给定映射下有 f:a→b,则 b 叫做a 的象,a 叫做b 的原象. 3、认知: 映射定义的精髓在于“任一(元素)对应唯一(元素)”,即 A 中任一元素在B 中都有唯一的象.在这里,A 中元素不可剩,允许B 中有剩余;不可“一对多”,允许“多对一”.因此,根据 B 中元素有无剩余的情况,映射又可分为“满射”和“非满射”两类. 集合A 到集合B 的映射 f:A→B 是一个整体,具有方向性; f:A→B 与 f:B→A 一般情况下是不同的映射. (三)、函数的表示法 表示函数的方法,常用的有解析法、列表法、图象法和口头描述法. 1、解析法:把两...