北师大版初一数学(下)讲义三角形(部分题目参考答案)

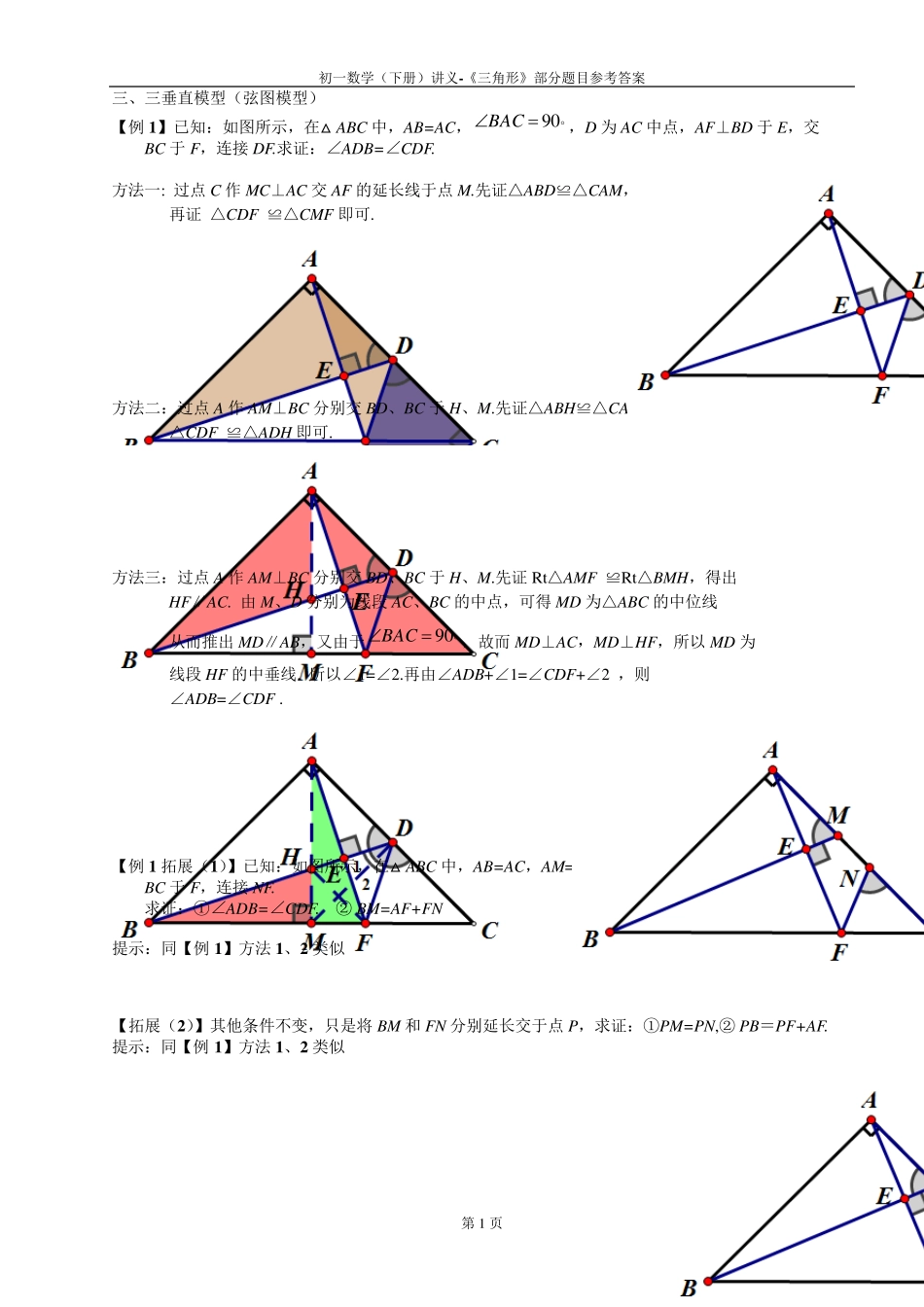
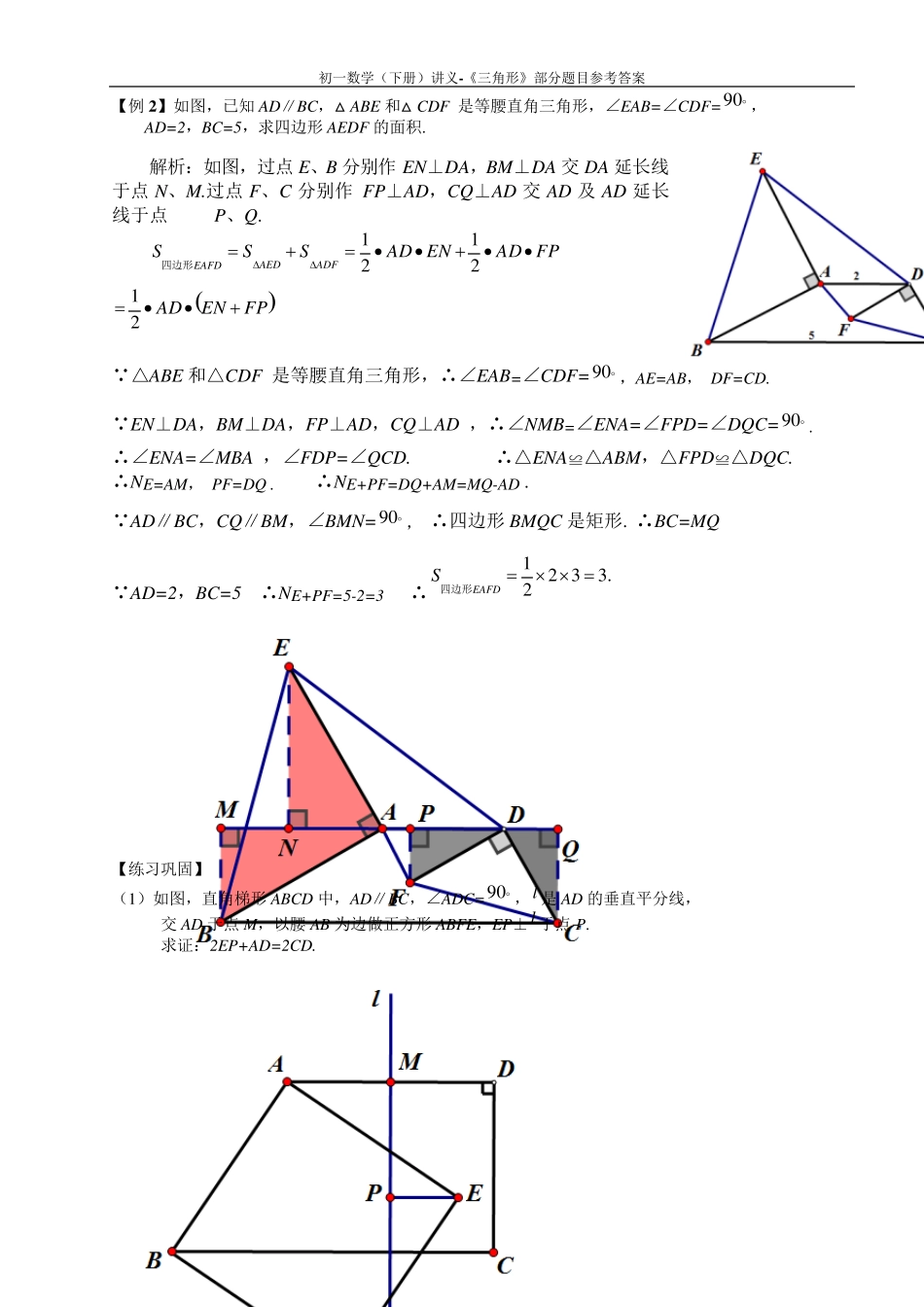
初一数学（下册）讲义-《三角形》部分题目参考答案 第1 页 三、三垂直模型（弦图模型） 【例1 】已知：如图所示，在△ABC 中，AB=AC，90 BAC，D 为AC 中点，AF⊥BD 于E，交 BC 于F，连接DF.求证：∠ADB=∠CDF. 方法一: 过点C 作 MC⊥AC 交AF 的延长线于点M.先证△ABD≌△CAM， 再证 △CDF ≌△CMF 即可. 方法二：过点A 作 AM⊥BC 分别交BD、BC 于H、M.先证△ABH≌△CAF， 再证 △CDF ≌△ADH 即可. 方法三：过点A 作 AM⊥BC 分别交BD、BC 于H、M.先证Rt△AMF ≌Rt△BMH，得出 HF∥AC. 由 M、D 分别为线段 AC、BC 的中点，可得 MD 为△ABC 的中位线 从而推出 MD∥AB，又由于90 BAC，故而 MD⊥AC，MD⊥HF，所以 MD 为 线段 HF 的中垂线. 所以∠1=∠2.再由∠ADB+∠1=∠CDF+∠2 ，则 ∠ADB=∠CDF . 【例1 拓展（1 ）】已知：如图所示，在△ABC 中，AB=AC，AM=CN，AF⊥BM 于E，交 BC 于F，连接NF. 求证：①∠ADB=∠CDF. ② BM=AF+FN 提示：同【例1 】方法 1 、2 类似 【拓展（2 ）】其他条件不变，只是将 BM 和 FN 分别延长交于点P，求证：①PM=PN,② PB＝PF+AF. 提示：同【例1 】方法 1 、2 类似 初一数学（下册）讲义-《三角形》部分题目参考答案 第2 页 【例2 】如图，已知AD∥BC，△ABE 和△CDF 是等腰直角三角形，∠EAB=∠CDF=9 0 ， AD=2，BC=5，求四边形AEDF 的面积. 解析：如图，过点 E、B 分别作 EN⊥DA，BM⊥DA 交 DA 延长线于点 N、M.过点 F、C 分别作 FP⊥AD，CQ⊥AD 交 AD 及 AD 延长线于点 P、Q. FPADENADSSSADFAEDEAFD2121四边形 FPENAD 21 △ABE 和△CDF 是等腰直角三角形，∴∠EAB=∠CDF=9 0 ，AE=AB， DF=CD. EN⊥DA，BM⊥DA，FP⊥AD，CQ⊥AD ，∴∠NMB=∠ENA=∠FPD=∠DQC=9 0 . ∴∠ENA=∠MBA ，∠FDP=∠QCD. ∴△ENA≌△ABM，△FPD≌△DQC. ∴NE=AM， PF=DQ . ∴NE+PF=DQ+AM=MQ-AD . AD∥BC，CQ∥BM，∠BMN=9 0 ， ∴四边形BMQC 是矩形. ∴BC=MQ AD=2，BC=5 ∴NE+PF=5-2=3 ∴.33221EAFDS四边形 【练习巩固】 （1 ）如图，直角梯形ABCD 中，AD∥BC，∠ADC=9 0 ，l是AD 的垂直平分线， 交 AD 于点 M，以腰AB 为边做正方形ABFE，EP⊥l于点 P. 求证：2EP+AD=2CD. 初一数学（下册）讲义-《三...