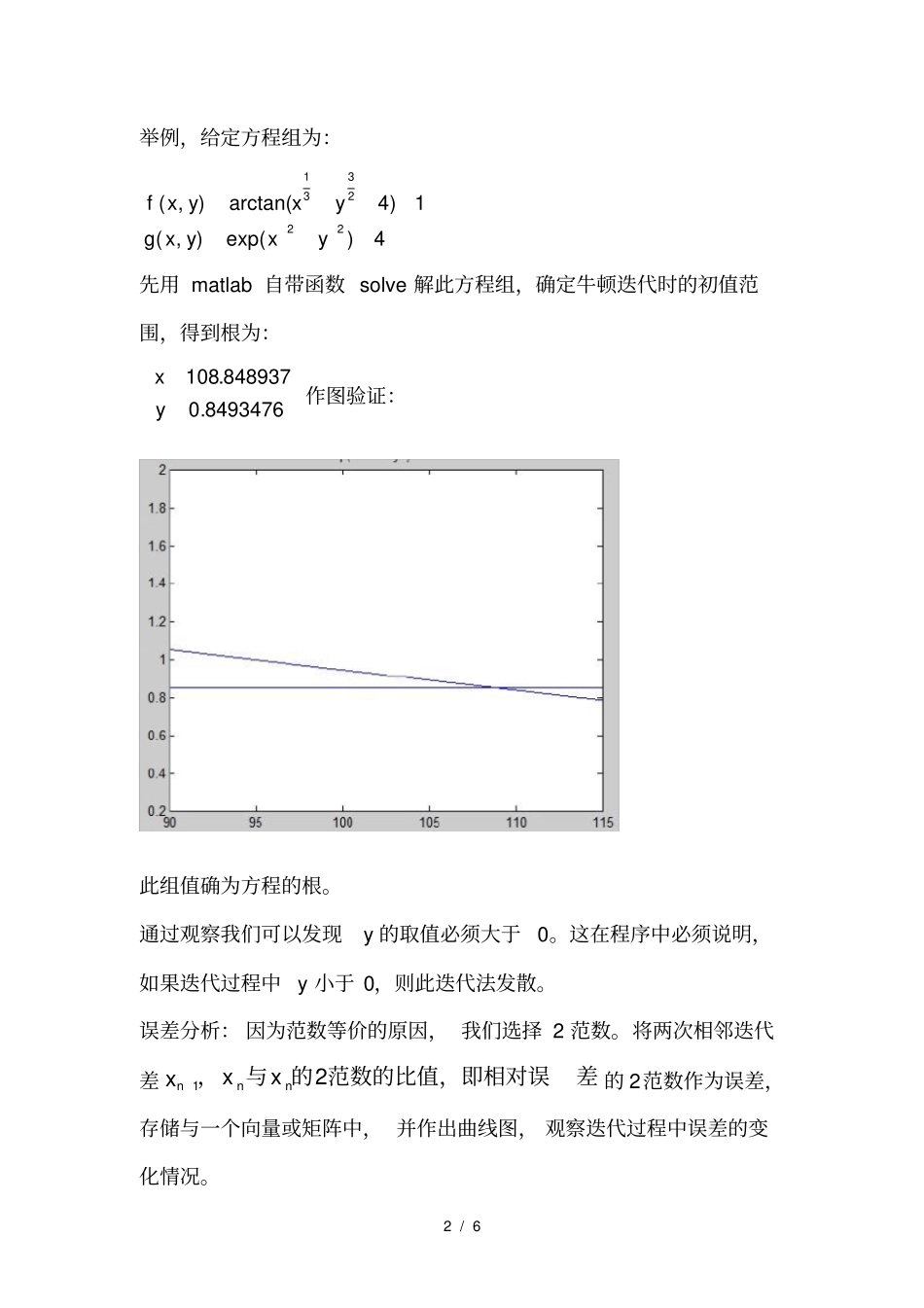
1 / 6 ),....,(,.0],;,[0),()(),()(),(0),()(),()(),(,.**,0],;,[),()()(),()()(,0),(),(),(])()[(),(),(),(),(),(])()[(),(),(2,),(])()[(21),(])()[(),(),()(2)(''))((')()(:11001n1n11010101010000000000000000000000000020000000000000000yxyxgfgffggfyygfgfgffgxxggffyxgyyyxgxxyxgyxfyyyxfxxyxfyxyxyxgfgffggfyygfgfgffgxxgfgffggfyygfgfgffgxxggffyxgyxgyyyxgxxyxfyxfyyyxfxxyxgyxfyxgyyyxxxyxgyxgyxfyxgyxfyyyxxxyxfyxfyxyxfyyyxxxyxfyyyxxxyxfyxfxxfxxxfxfxfxyyxxxnnxyyxyyyxyxnnynnnxnnnnnynnnxnnnnnxyyxxxxyyxyyxyyxxxxyyxyyyxyxyxyxyyxxyyxxyxyyxx),由此可得到迭代序列(,则其解可记为:的行列式不为若系数矩阵:附近的线性化方程组为在一元方程牛顿迭代法,类似,的新近似值于是就得到了根,则可得解:的行列式不为若系数矩阵),(),(),(),(则两式构成方程组:令可得:构成二元方程组,同样与若另有一方程:阶小项,得到线性方程忽略在方程根附近取值时,当二元函数的展开为:开类似一元函数的泰勒展2 / 6 举例,给定方程组为:4)exp(),(1)4arctan(),(222331yxyxgyxyxf先用 matlab 自带函数 solve 解此方程组,确定牛顿迭代时的初值范围,得到根为:8493476.0848937.108yx作图验证:此组值确为方程的根。通过观察我们可以发现y 的取值必须大于0。这在程序中必须说明,如果迭代过程中y 小于 0,则此迭代法发散。误差分析: 因为范数等价的原因, 我们选择 2 范数。将两次相邻迭代差差范数的比值,即相对误的与,2xxnn1nx的 2范数作为误差,存储与一个向量或矩阵中, 并作出曲线图, 观察迭代过程中误差的变化情况。3 / 6 如选初值为 (12,0.3),得到误差图形为:选初值为 (12,1.2),误差图为:我们可以发现误差在前3-5 次迭代的时候迅速下降,但是中间会有上升的过程,直至最后误差达到我们设定的误差值。由此猜想迭代过程可能漏掉了一些根,利用作图,得到曲线如下:4 / 6 可以发现还有两组根, 用牛顿迭代法只能得到一组值,可能是因为所给方程比较特殊,它的定义域中x,y 均不能为 0,导致函数不连续。另外,也可能因为函数不连续, 导致初值只能在根的附件变化时才能得到收敛的结果。因此我们不妨将初值选的稍微小一些,如:[1,2],得到根为2.7637y0.8925x选初值为 [-1,4],得到根为5 / 6 3.4880y-0.8757x综上所述,此方程组有三组根, 不同的初值,会得到不同的解的情况,也会...