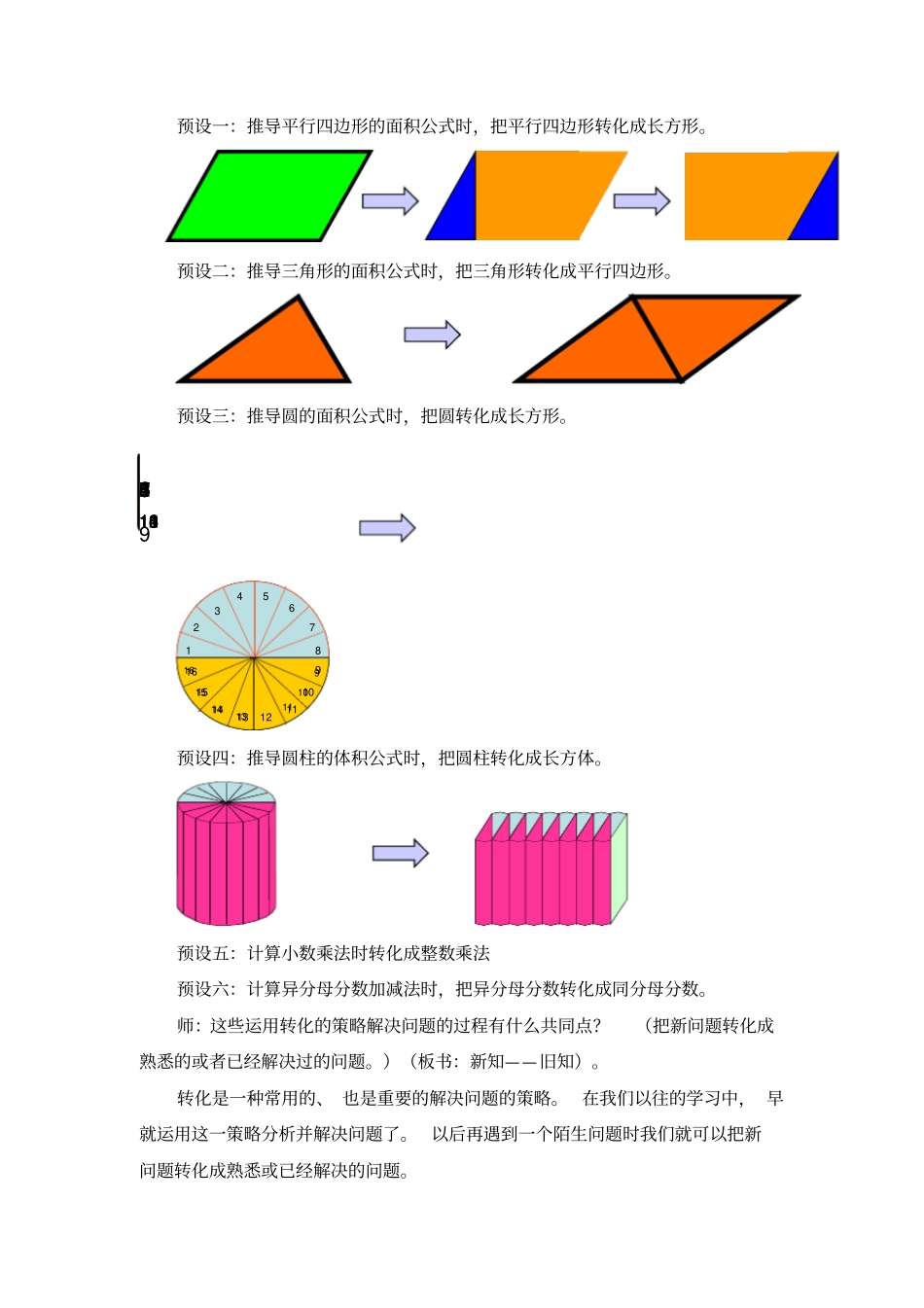
用转化的策略解决问题教学目标 : 1. 教材让学生在直观的情境中想到转化,并应用图形的平移和旋转知识进行图形的等积,等周长的变形. 2. 在解决实际问题过程中体会转化的含义和应用的手段,感受转化在解决这个问题时的价值。3. 进一步积累解决问题的经验, 增强解决问题的 " 转化 "意识 , 提高学好数学的信心 . 教学重点 : 感受“转化”策略的价值,会用“转化”的策略解决问题。教学难点:会用“转化”的策略解决问题。教学准备:多媒体课件、作业纸教学过程预设:一、观察比较,感知“转化”(课件出示例 1)教师:这两幅图的面积大小你能直接告诉我吗?(1)引导猜测:那请您猜猜看,这两幅图的面积谁大谁小?你觉得这两幅图形的面积相等吗?(学生猜测)你会想办法来验证你的猜测是否正确吗?(2)学生独立思考,可以利用手中的练习纸涂涂画画。然后四人小组交流各自的思考过程。(3)交流反馈验证情况。学生口述过程,教师配以课件演示。 (可能有的方法是:数格子和转化成长方形比较。)追问:( 1)第一个图形是怎样转化成长方形的?你是怎样想到把上面的半圆进行平移的?上面的半圆向什么方向平移了几格?(2)第二个图形是怎样转化成长方形的?你是怎样想到把左右两个半圆进行旋转的?左右两个半圆分别按什么方向旋转了多少度?(4)课件再次演示“转化”过程。边演示,师生边共同叙述转化过程: 把半圆向下平移5 格后第一幅图转化成了长方形; 把左右两个半圆旋转180 度后第二幅图转化成了长方形; 两个长方形面积相等,所以两幅图的面积就相等。(5)小结转化方法追问:在 2 副图变化的过程中,他们什么没有发生变化?(面积)什么发生了变化?(形状)在这个过程中,我们把两幅不规则图形转化成面积不变的长方形后来比较大小,在解决问题的过程中我们运用了什么策略?(转化)板书课题。我们为什么要把两幅图形都转化成长方形呢?(这样更容易比较大小)(板书:不规则图形——规则图形)。引导学生回答:转化可以化繁为简。二、回顾知识,体验“转化”师引导:在以往的学习中, 我们曾经就运用转化的策略解决过一些问题,回忆一下。同桌交流。学生充分列举,教师课件配合演示。预设一:推导平行四边形的面积公式时,把平行四边形转化成长方形。预设二:推导三角形的面积公式时,把三角形转化成平行四边形。预设三:推导圆的面积公式时,把圆转化成长方形。预设四:推导圆柱的体积公式时,把圆柱转化成长方体...