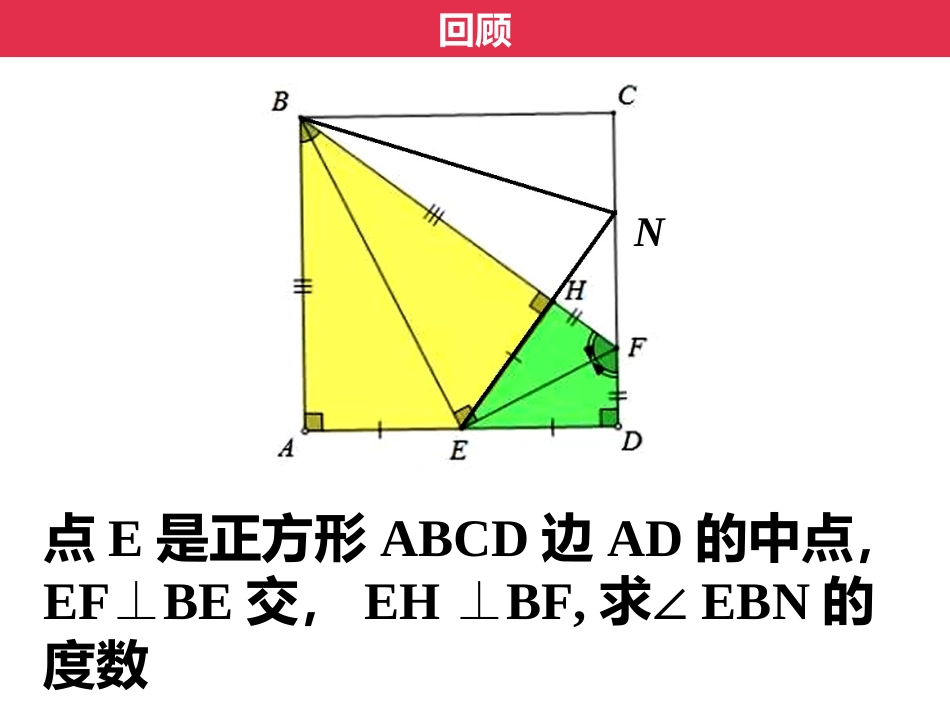
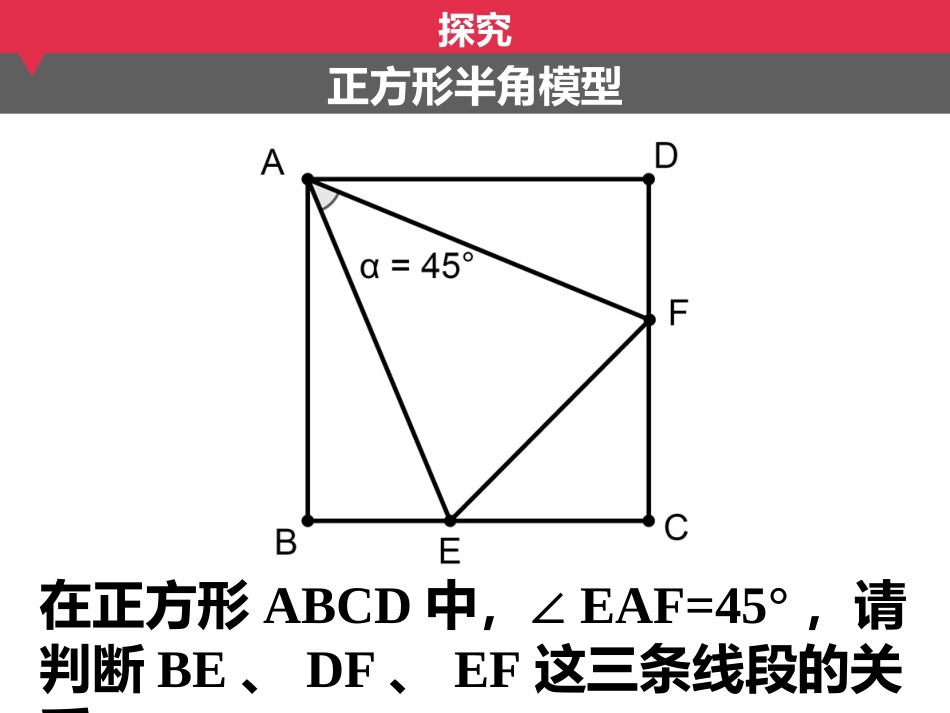
石台中学九零一班中考专题突破——半角模型回顾点E是正方形ABCD边AD的中点,EFBE⊥交,EHBF,⊥求∠EBN的度数N探究在正方形ABCD中,∠EAF=45°,请判断BE、DF、EF这三条线段的关系正方形半角模型探究在正方形ABCD中,∠EAF=45°,则BE+DF=EF正方形半角模型练习正方形半角模型如图,正方形ABCD的边长为2,点E、F分别在边AB、CD上,∠EBF=45°则△EDF的周长等于探究在正方形ABCD中,∠EAF=45°,请判断BM、MN、DN这三条线段的关系正方形半角模型探究在正方形ABCD中,∠EAF=45°,则BM²+DN²=MN²正方形半角模型探究正方形半角模型在正方形ABCD中,∠EAF=45°,则BM²+DN²=MN²探究在等腰直角△ABD中,∠EAF=45°,则BM²+DN²=MN²等腰直角三角形半角模型等腰直角三角形半角模型练习在△ABC中,ADBC⊥于点D,BAC∠=45°,BD=3,DC=2,则△ABC的面积为等腰直角三角形半角模型练习在△ABC中,ADBC⊥于点D,BAC=45°,∠BD=3,DC=2,则△ABC的面积为探究正方形半角模型半角模型基本结论:BE+DF=EF、BM²+DN²=MN²