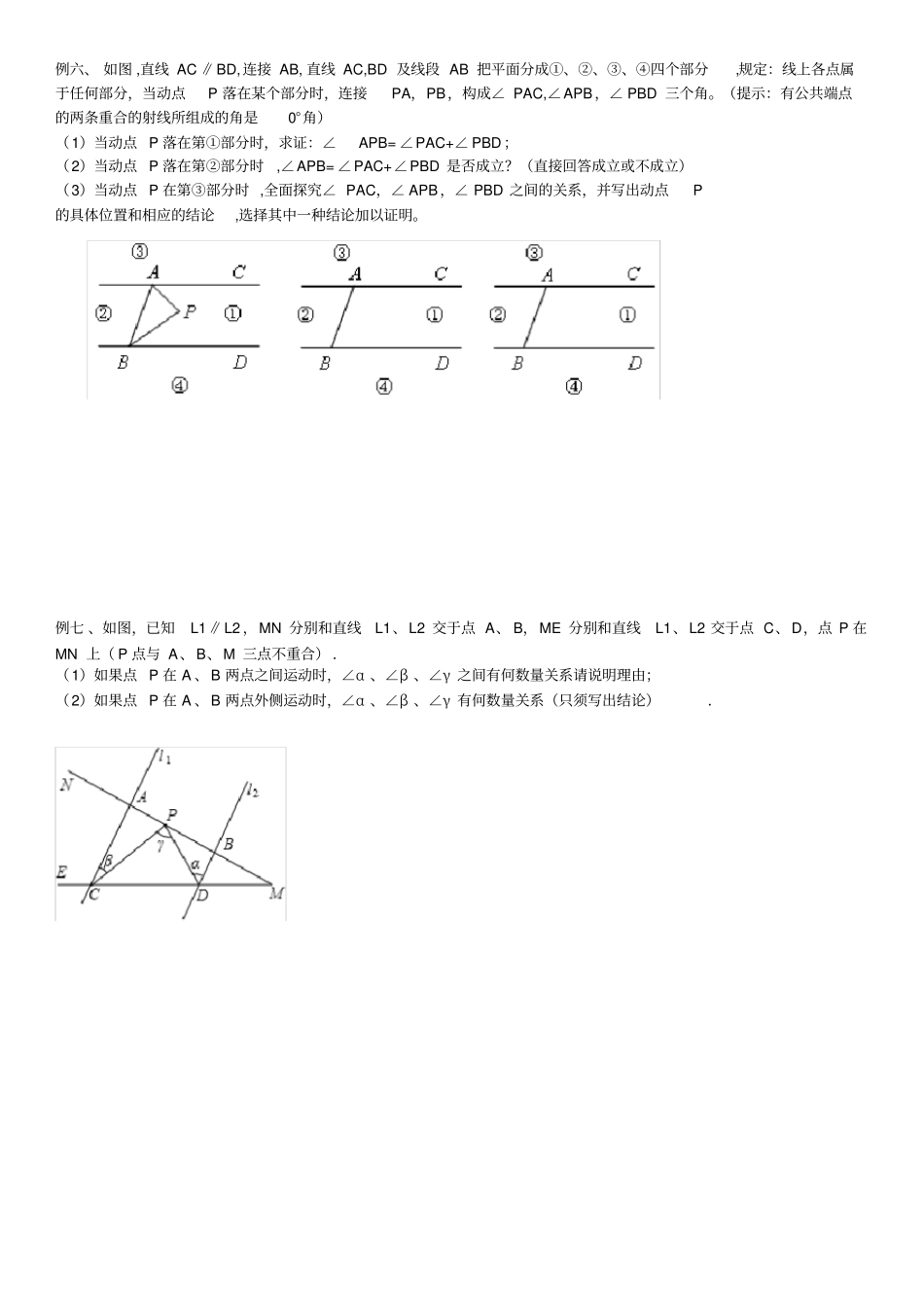
《相交线与平行线》培优综合训练例一、 如图, AB ∥CD ,EF 分别交 AB ,CD 于 M ,N,∠ EMB=50°,MG 平分∠ BMF ,MG 交 CD 于 G. 求∠ 1 的度数 . 例二 、已知:如图,CD⊥AB 于 D, DE∥BC,EF⊥AB 于 F,求证:∠ FED =∠ BCD .例三、 已知:如图∠ 1=∠2,∠ A 和∠ F,请问∠ C=∠D 相等吗?试写出推理过程。例四 、已知:如图,∠ABC 和∠ ACB 的平分线交于点O,EF 经过点 O 且平行于 BC,分别与 AB,AC 交于点(1)若∠ ABC=50°,∠ ACB=60°,求∠ BOC 的度数;(2)若∠ ABC=а,∠ ACB=β,用 а,β 的代数式表示∠BOC 的度数.(3)在第 (2)问的条件下, 若∠ ABC 和∠ ACB 邻补角的平分线交于点O,其他条件不变, 请画出相应图形, 并用 а,β的代数式表示∠BOC 的度数.例五、 已知:∠ A= (90+x) °,∠ B= (90﹣x)°,∠CED=90°,射线 EF∥AC ,2∠C﹣∠ D=m°(1)判断 AC 与 BD 的位置关系,并说明理由.(2)如图 1,当 m=30° 时,求∠ C、∠ D 的度数.(3)如图 2,求∠ C、∠ D 的度数(用含m 的代数式表示)例六、 如图 ,直线 AC ∥BD,连接 AB, 直线 AC,BD 及线段 AB 把平面分成①、②、③、④四个部分,规定:线上各点属于任何部分,当动点P 落在某个部分时,连接PA,PB,构成∠ PAC,∠APB,∠ PBD 三个角。(提示:有公共端点的两条重合的射线所组成的角是0°角)(1)当动点 P 落在第①部分时,求证:∠APB= ∠PAC+∠ PBD;(2)当动点 P 落在第②部分时,∠APB= ∠PAC+∠PBD 是否成立?(直接回答成立或不成立)(3)当动点 P 在第③部分时 ,全面探究∠ PAC,∠ APB,∠ PBD 之间的关系,并写出动点P 的具体位置和相应的结论,选择其中一种结论加以证明。例七 、如图,已知L1∥L2 ,MN 分别和直线L1、L2 交于点 A、 B,ME 分别和直线L1、L2 交于点 C、D,点 P 在MN 上( P 点与 A、B、M 三点不重合) .(1)如果点 P 在 A 、B 两点之间运动时,∠α 、∠β 、∠γ 之间有何数量关系请说明理由;(2)如果点 P 在 A 、B 两点外侧运动时,∠α 、∠β 、∠γ 有何数量关系(只须写出结论).培优练习1、如图,把矩形 ABCD 沿 EF 对折后使两部分重合,若150° ,则AEF =()2、如图,将三角尺的直角顶点放在直尺的一边上,130250°,° ...