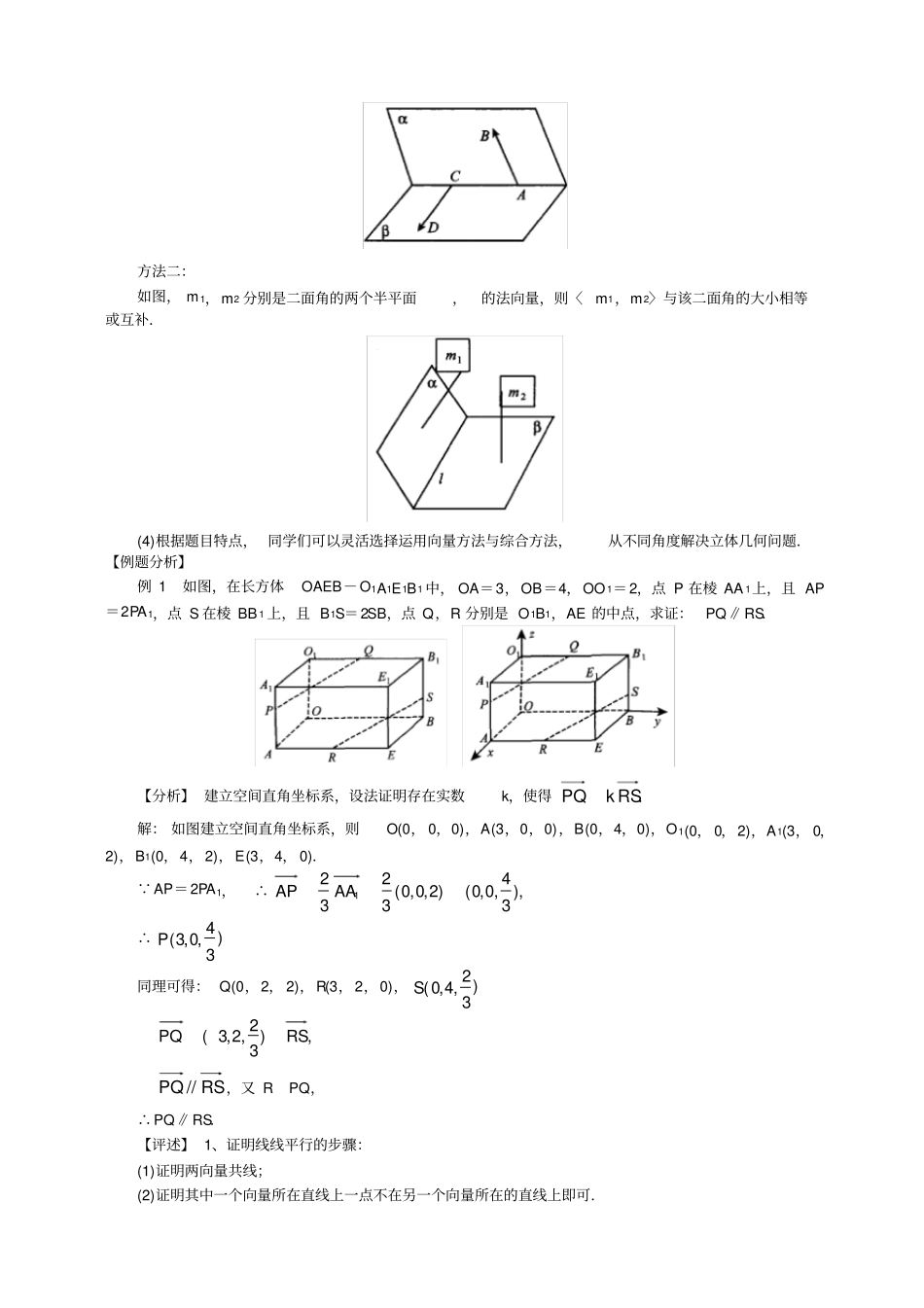
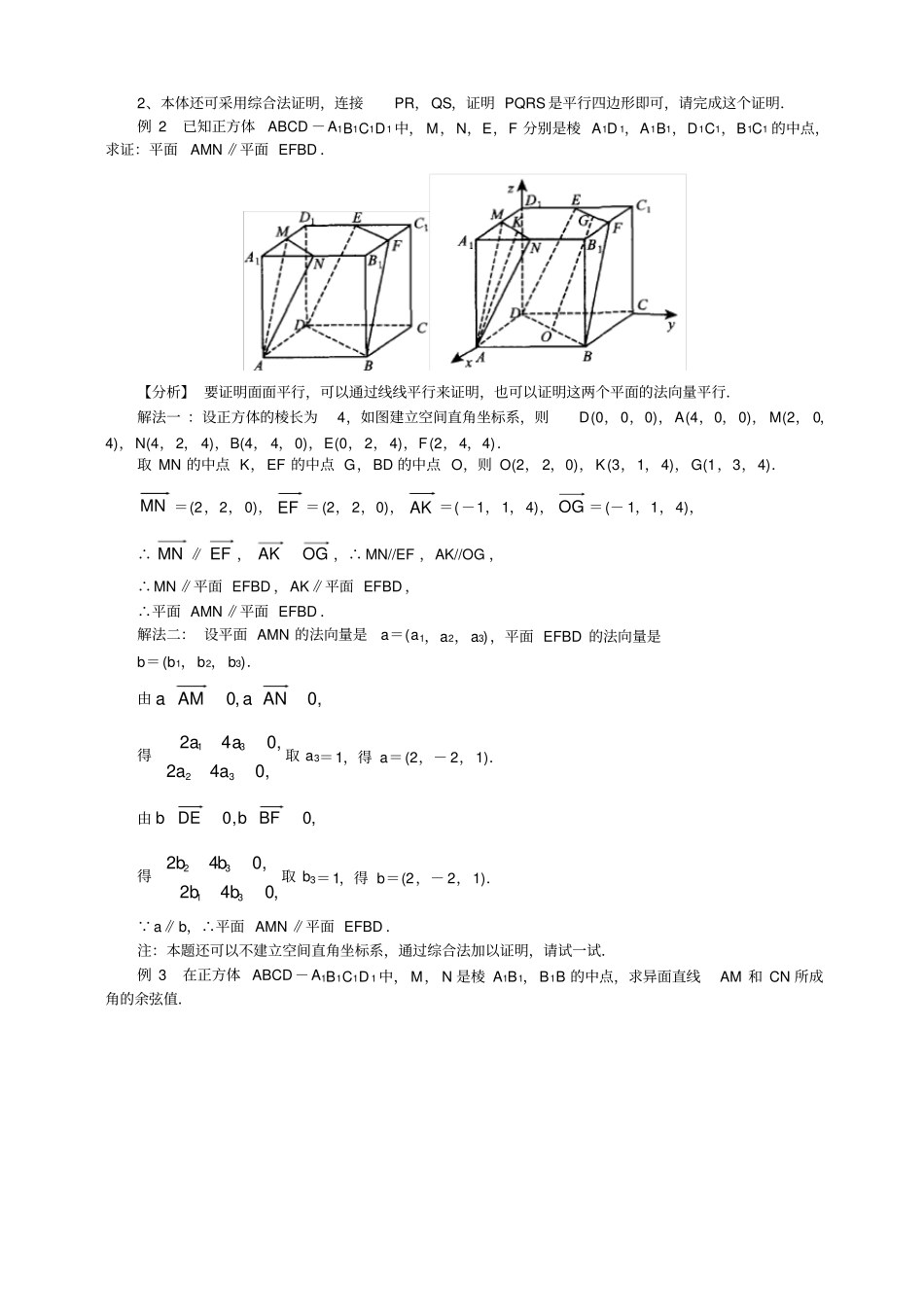
空间向量在立体几何中的应用:(1)直线的方向向量与平面的法向量:①如图, l 为经过已知点A 且平行于已知非零向量a 的直线,对空间任意一点O,点 P 在直线 l 上的充要条件是存在实数t,使得atOAOP,其中向量a 叫做直线的 方向向量 .由此可知,空间任意直线由空间一点及直线的方向向量惟一确定.②如果直线l⊥平面,取直线 l 的方向向量a,则向量 a 叫做平面的 法向量 .由此可知,给定一点A 及一个向量a,那么经过点A 以向量 a 为法向量的平面惟一确定.(2)用空间向量刻画空间中平行与垂直的位置关系:设直线 l,m 的方向向量分别是a,b,平面,的法向量分别是u,v,则①l∥ma∥ba=kb,k∈R;②l⊥ma⊥ba·b=0;③l∥a⊥ua·u=0;④l⊥a∥ua= ku,k∈R;⑤∥u∥vu=kv,k∈R;⑥⊥u⊥vu·v=0.(3)用空间向量解决线线、线面、面面的夹角问题:①异面直线所成的角:设a,b 是两条异面直线,过空间任意一点O 作直线 a′ ∥a,b′ ∥ b,则 a′与 b′ 所夹的锐角或直角叫做异面直线a 与 b 所成的角.设异面直线a 与 b 的方向向量分别是v1,v2,a 与 b 的夹角为,显然],2π,0(则|||||||,cos|212121vvvvvv②直线和平面所成的角:直线和平面所成的角是指直线与它在这个平面的射影所成的角.设直 线 a 的方向向量是u , 平面的法向 量是v ,直 线 a 与平面的夹角 为,显然]2π,0[,则|||||||,cos|vuvuvu③二面角及其度量:从一条直线出发的两个半平面所组成的图形叫做二面角.记作- l-在二面角的棱上任取一点O,在两个半平面分别作射线OA⊥l,OB⊥l,则∠ AOB 叫做二面角-l-的平面角.利用向量求二面角的平面角有两种方法:方法一:如图,若 AB, CD 分别是二面角- l-的两个面与棱l 垂直的异面直线,则二面角-l-的大小就是向量CDAB与的夹角的大小.方法二:如图, m 1,m2 分别是二面角的两个半平面,的法向量,则〈m1,m 2〉与该二面角的大小相等或互补.(4)根据题目特点, 同学们可以灵活选择运用向量方法与综合方法,从不同角度解决立体几何问题.【例题分析】例 1如图,在长方体OAEB-O1A1E1B1 中, OA=3,OB=4,OO 1=2,点 P 在棱 AA 1上,且 AP=2PA1,点 S 在棱 BB 1 上,且 B1S=2SB,点 Q,R 分别是 O1B1,AE 的中点,求证:PQ∥RS.【分析】 建立空间直角坐标系,设法证明存在实数k,使得.RSkPQ解: 如图建立空间直角坐标系,则O(0,...