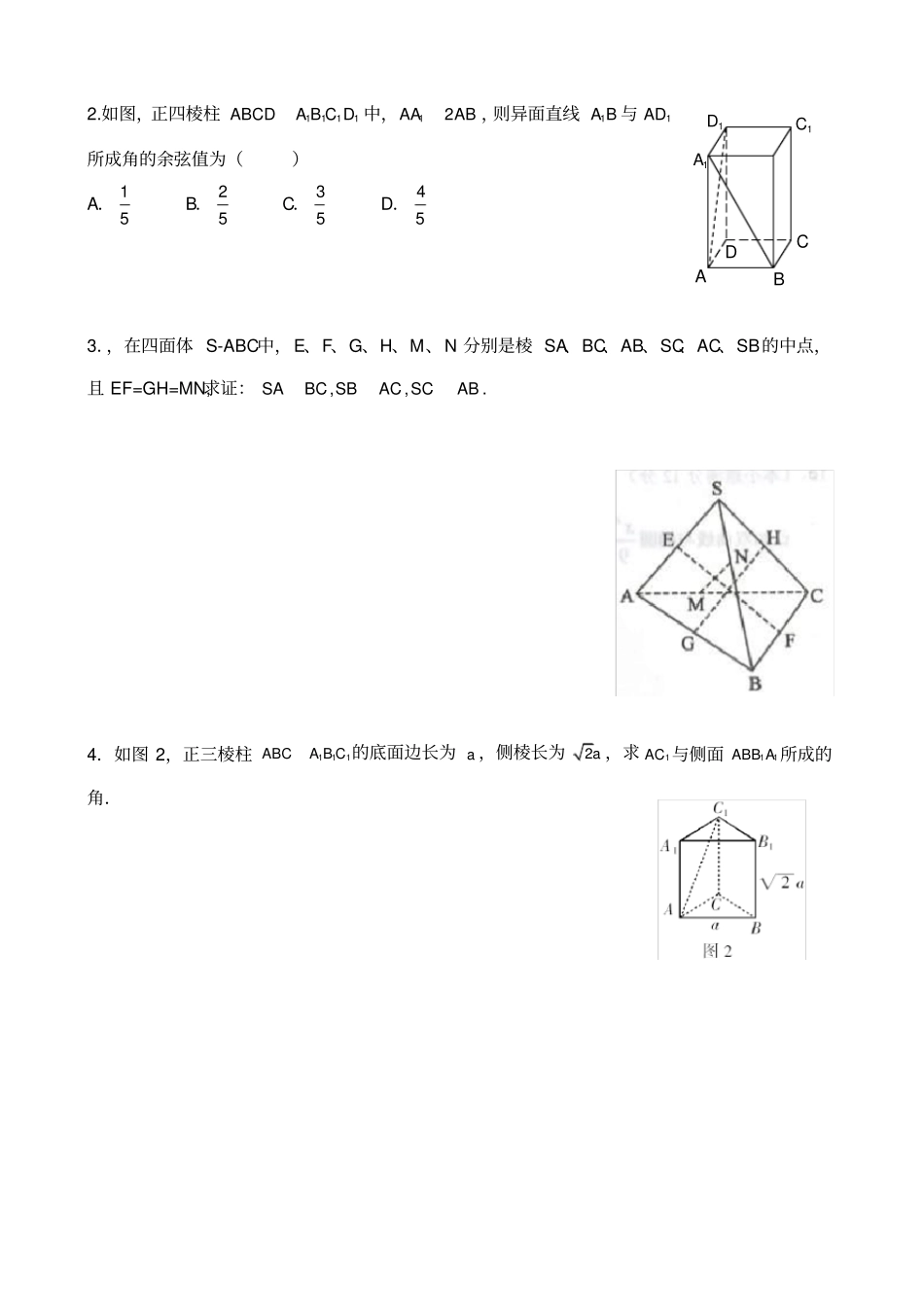
向量的数量积和坐标运算ba,是两个非零向量,它们的夹角为,则数cos||||ba叫做 a 与 b 的数量积(或内积),记作ba,即.cos||||baba其几何意义是 a 的长度与 b 在 a 的方向上的投影的乘积. 其坐标运算是:若),,(),,,(222111zyxbzyxa,则①212121zzyyxxba;②222222212121||,||zyxbzyxa;③212121zzyyxxba④222222212121212121,coszyxzyxzzyyxxba. 异面直线nm,所成的角分别在直线nm,上取定向量,,ba则异面直线nm,所成的角等于向量ba,所成的角或其补角(如图 1 所示),则.||||||cosbaba. 异面直线nm、 的距离分别在直线nm、 上取定向量,, ba求与向量ba、都垂直的向量 n ,分别在nm、 上各取一个定点BA、,则异面直线nm、 的距离 d 等于 AB 在 n 上的射影长,即||||nnABd.. 直线 L 与平面所成的角在 L 上取定 AB ,求平面的法向量 n(如图 2 所示),再求||||||cosnABnAB,则2为所求的角 . Cn图1DABnmab. 二面角方法一:构造二面角l的两个半平面、 的法向量21nn 、(都取向上的方向,如图3 所示),则①若二面角l是“钝角型”的如图3 甲所示 , 那么其大小等于两法向量21nn 、的夹角的补角,即.||||cos2121nnnn(例如 2004 年高考数学广东卷第 18 题第( 1)问) .② 若二面角l是“锐角型” 的如图 3 乙所示, 那么其大小等于两法向量21nn 、的夹角,即.||||cos2121nnnn③ 方法二:在二面角的棱 l 上确定两个点BA、,过BA、分别在平面、 内求出与 l 垂直的向量21nn 、(如图 4 所示),则二面角l的大小等于向量21nn 、的夹角,即.||||cos2121nnnn. 平面外一点 p 到平面的距离先求出平面的法向量 n ,在平面内任取一定点A,则点 p 到平面的距离 d 等于 AP 在 n 上的射影长,即||||nnAPd.练习1.在长方体1111ABCDA B C D 中,1B C 和1C D 与底面所成的角分别为60° 和 45° ,则异面直线1B C和1C D 所成角的余弦值为.1n2n图 3乙l1n2nl图 3甲1n2nl图4BA图5Apn2.如图,正四棱柱1111ABCDA B C D 中,12AAAB ,则异面直线1A B 与1AD所成角的余弦值为()A. 15B. 25C. 35D. 453.,在四面体 S-ABC中,E、F、G、H、M、N 分别是棱 SA、BC、AB、SC、AC、SB的中点,且 EF=GH=MN,求证:ABSCACSBBCSA,,.4.如图 2,正三棱柱111ABCA B C 的底面边长为 a ,侧棱长为2a ,求1AC 与侧面11ABB A 所成的角.AB1A1D1CCD5.如图 3,直...