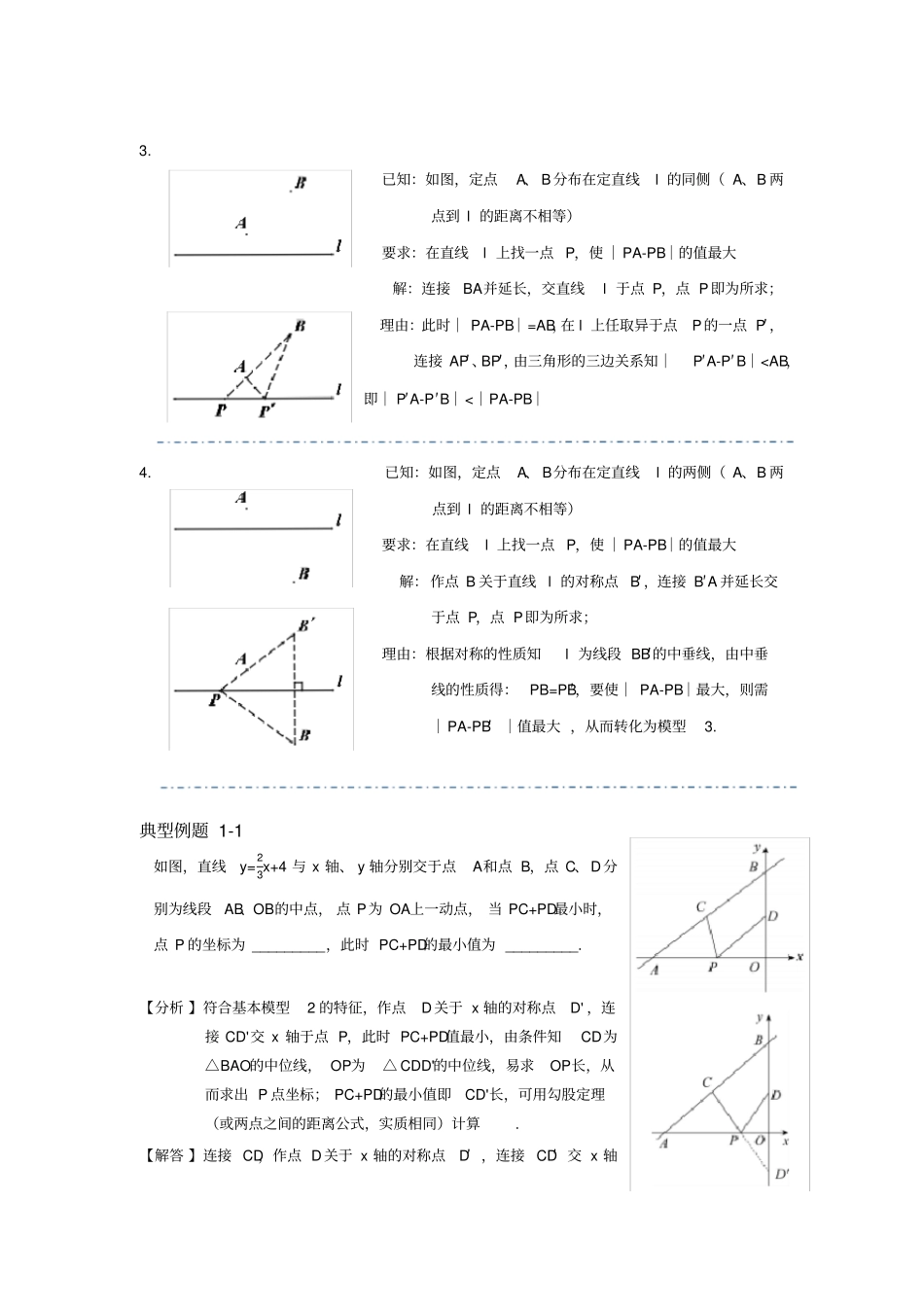
将军饮马问题问题概述路径最短、线段和最小、线段差最大、周长最小等一系列最值问题方法原理1. 两点之间,线段最短;2. 三角形两边之和大于第三边,两边之差小于第三边;3. 中垂线上的点到线段两端点的距离相等;4. 垂线段最短 .基本模型1. 已知:如图,定点A、B 分布在定直线l 两侧;要求:在直线l 上找一点 P,使 PA+PB的值最小解:连接 AB交直线 l 于点 P,点 P即为所求 , PA+PB的最小值即为线段AB的长度理由:在 l 上任取异于点P 的一点 P′,连接 AP′、BP′,在△ ABP’中, AP′+BP′>AB,即 AP′+BP′>AP+BP ∴P 为直线 AB与直线 l 的交点时, PA+PB最小 . 2.已知:如图,定点A 和定点 B在定直线 l 的同侧要求:在直线l 上找一点 P,使得 PA+PB值最小(或△ ABP的周长最小)解:作点 A关于直线 l 的对称点 A′,连接 A′B 交 l 于 P,点 P 即为所求;理由:根据轴对称的性质知直线l 为线段 AA′的中垂线,由中垂线的性质得:PA=PA′,要使 PA+PB最小,则需 PA′+PB值最小,从而转化为模型1. 3.已知:如图,定点A、 B分布在定直线l 的同侧( A、B 两点到 l 的距离不相等)要求:在直线l 上找一点 P,使 ︱PA-PB︱的值最大解:连接BA并延长,交直线l 于点 P,点 P即为所求;理由:此时︱ PA-PB︱=AB,在 l 上任取异于点P的一点 P′,连接 AP′、BP′,由三角形的三边关系知︱P′A-P′B︱