内江市2013届高中三年级第二次模拟考试试题理数VIP免费

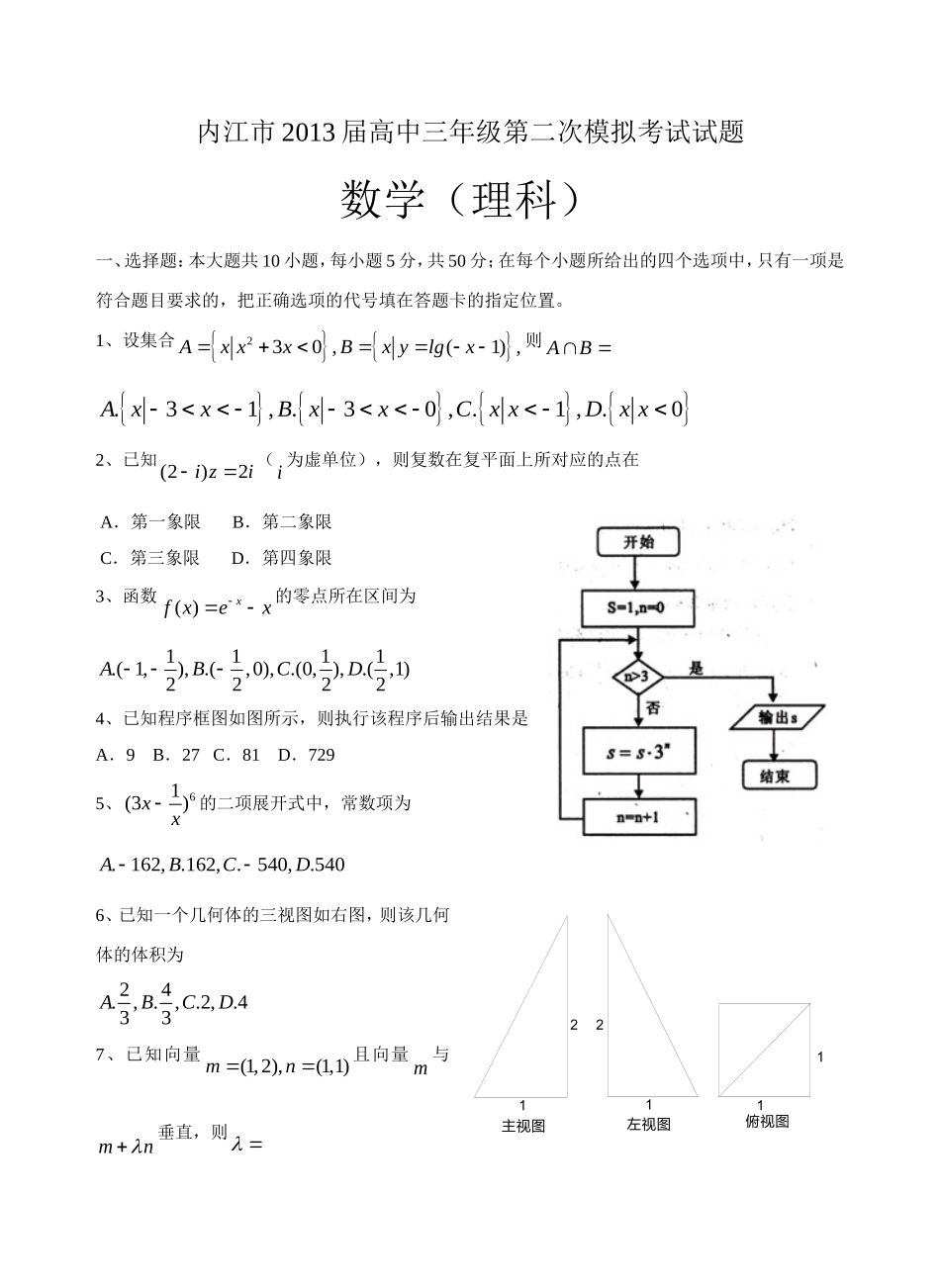
内江市2013届高中三年级第二次模拟考试试题数学（理科）一、选择题：本大题共10小题，每小题5分，共50分；在每个小题所给出的四个选项中，只有一项是符合题目要求的，把正确选项的代号填在答题卡的指定位置。1、设集合230,(1),AxxxBxylgx则AB.31,.30,.1,.0AxxBxxCxxDxx2、已知(2)2izi（i为虚单位），则复数在复平面上所对应的点在A．第一象限B．第二象限C．第三象限D．第四象限3、函数()xfxex的零点所在区间为1111.(1,),.(,0),.(0,),.(,1)2222ABCD4、已知程序框图如图所示，则执行该程序后输出结果是A．9B．27C．81D．7295、61(3)xx的二项展开式中，常数项为.162,.162,.540,.540ABCD6、已知一个几何体的三视图如右图，则该几何体的体积为24.,.,.2,.433ABCD7、已知向量(1,2),(1,1)mn�且向量m�与mn�垂直，则112121俯视图左视图主视图3535.,.,.,.5353ABCD8、某公司计划在甲、乙两个电视台做总时间不超过300分钟的广告，广告费用不超过9万元，甲、乙电视台的广告费标准分别是500元/分钟和200元/分钟，假设甲、乙两个电视台为该公司做的广告能给公司带来的收益分别为0.3万元和0.2万元，那么该公司合理分配在甲、乙两个电视台的广告时间，能使公司获得最大的收益是A．90万元B．80万元C．70万元D．60万元9、若函数()fx对任意实数x满足(1)()fxfx且1,0x时，()fxx，则函数()yfx的图象与3logyx的图象的交点个数为A．2B．3C．4D．510、过椭圆C：2215xy的右焦点F作直线l交椭圆C于A、B两点，交y轴于点M，若12,MAAFMBBF�，则12.10,.5,.5,.10ABCD二、填空题：本大题共5个小题，每小题5分，共计25分。请把答案填在答题卡上的相应横线上。11、已知3cos(0)5，则sin()_____________6。12、若直线1ykx与圆O：221xy交于A、B两点，且60AOB，则实数_________k13、已知三棱锥111ABCABC的底面是边长为6的正三角形，侧棱垂直底面且侧棱长为2，则该三棱锥的外接球表面积是_________14、从10名大学毕业生中选3人担任村长助理，则甲、乙至少有1人入选，而丙没有入选的概率是_________15、在实数集R中定义一种运算“”，对任意,,abRab为唯一确定的实数且具有性质：（1）对任意,abR，有abba；（2）对任意aR，有0aa；（3）对任意,,abcR，有()()()()2abccabaccbc。已知函数221()fxxx，则下列命题中：（1）函数()fx的最小值为3；（2）函数()fx为奇函数；（3）函数()fx的单调递增区间为1,0、(1,)。其中正确例题的序号有_________三、解答题：本大题共6个小题，共75分.解答应写出文字说明、证明过程或演算步骤。16、（本题满分12分）设ABC的内角A、B、C所对应的边分别为cba,,，2,54cosbB（1）当6A时，求a的值；（2）当ABC面积为3时，求ca的值。17、（本题满分12分）某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如右图：（1）比较这两名队员在比赛中得分的均值和方差的大小；（2）以上述数据统计，甲、乙两名队员得分超过15分的概率做为概率，假设甲、乙两名队员在比赛中得分多少互不影响，求本赛季接下来的2场比赛中，甲、乙两名队员得分均超过15分的场数的分布列和期望。18、（本题满分12分）如图，在多面体ABCDEF中，ABCD为菱形，60ABC，EC面ABCD，FA面ABCD，G为BF中点，//EG面ABCD。（1）求证：EG面ABF；（2）若ABAF，求二面角DEFB的余弦值。19、（本题满分12分）已知动圆P过定点)2,0(F，且与直线l相切，椭圆N的对称轴为坐标轴，一个焦点是F，点)2,1(A在椭圆N上。（1）求动圆圆心P的轨迹M的方程和椭圆N的方程；（2）已知与轨迹M在4x处的切线平行的直线与椭圆N交于B、C两点，试探求使ABC面积等于23的直线l是否存在？若存在，请求出直线l的方程；若不存在，请说明理由。乙甲3183975063318797210GFEDCBA20、（本题满分13分）已知数列na的前项和为ns，且52,511nssann（1）证明...