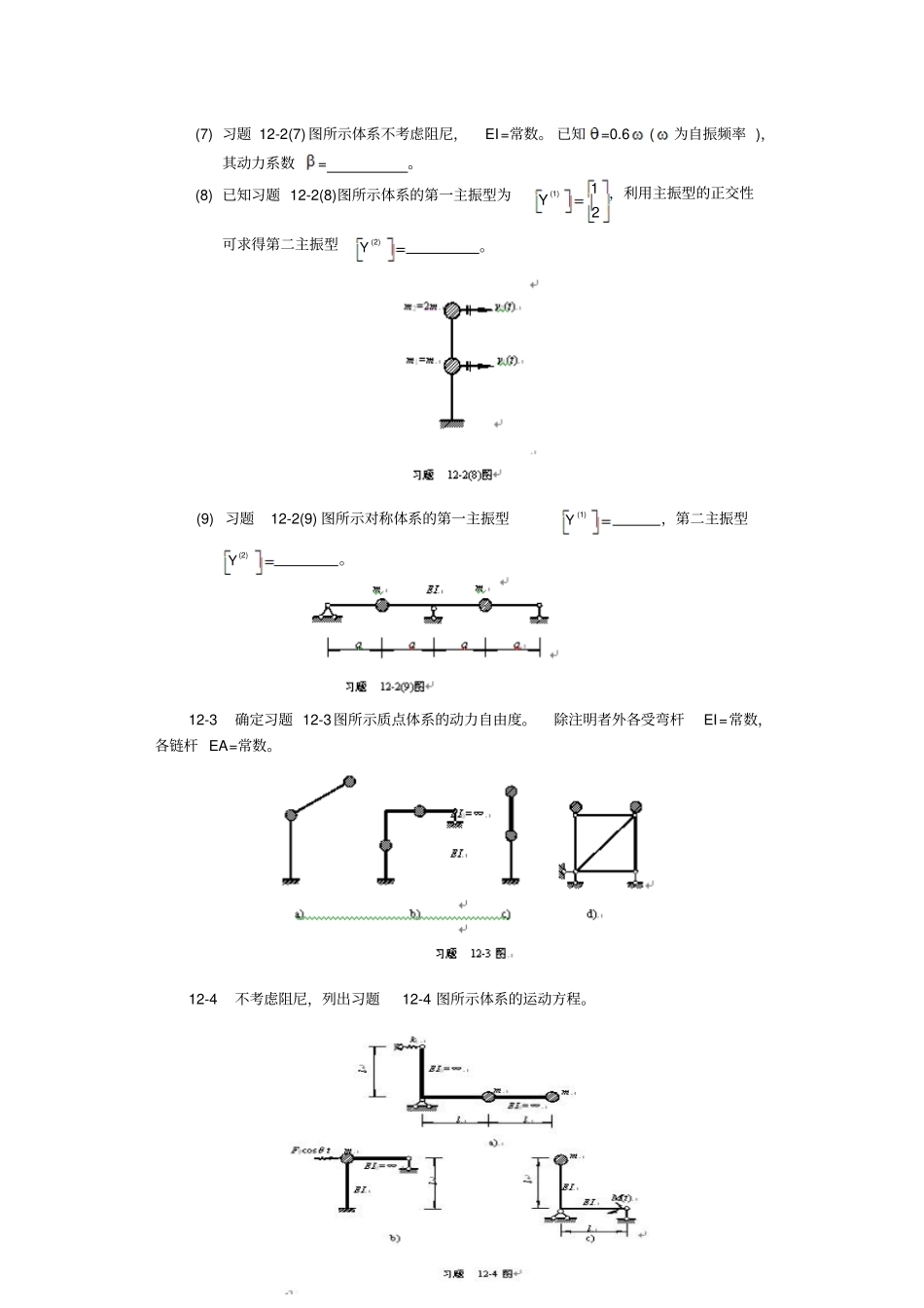
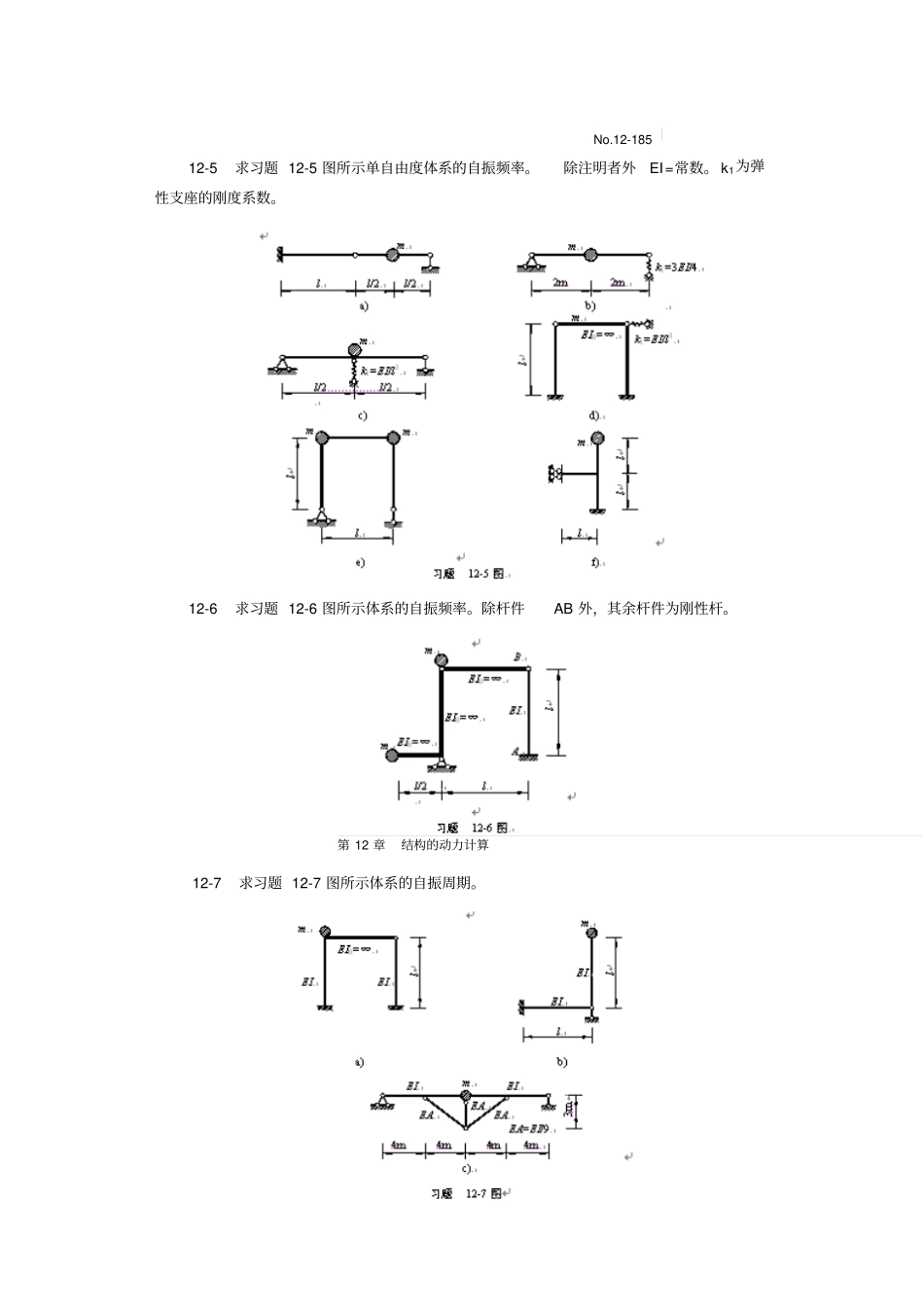
习题12-1 是非判断(1) 引起单自由度体系自由振动的初速度值越大,则体系的自振频率越大。() (2) 如果单自由度体系的阻尼增大,将会使体系的自振周期变短。( ) (3) 在土木工程结构中,阻尼对自振周期的影响很小。() (4) 由于各个质点之间存在几何约束,质点体系的动力自由度数总是小于其质点个数。 () (5) 多自由度体系的自振频率与引起自由振动的初始条件无关。() (6) n 个自由度体系有n 个自振周期,其中第一周期是最长的。( ) (7) 如果考虑阻尼, 多自由度体系在简谐荷载作用下的质点振幅就不能用列幅值方程的方法求解。 () 12-2 填空(1) 单自由度体系运动方程为2P2( ) /yyyFtm ,其中未考虑重力,这是因为。(2) 单自由度体系自由振动的振幅取决于:。(3) 若要改变单自由度体系的自振周期,应从改变体系的或着手。(4) 若由式 (12-23)求得的动力系数为负值。则表示。(5) 习题 12-2(5) 图所示体系发生共振时,干扰力与平衡。(6) 求习题 12-2(6)图所示质点系的自振频率时(EI =常数 ),其质量矩阵 [M]= 。第 12 章结构的动力计算m(7) 习题 12-2(7) 图所示体系不考虑阻尼,EI=常数。 已知=0.6(为自振频率 ),其动力系数= 。(8) 已知习题 12-2(8)图所示体系的第一主振型为(1)12Y,利用主振型的正交性可求得第二主振型(2)Y。(9) 习题12-2(9) 图所示对称体系的第一主振型(1)Y,第二主振型(2)Y。12-3 确定习题 12-3图所示质点体系的动力自由度。除注明者外各受弯杆EI=常数,各链杆 EA=常数。12-4不考虑阻尼,列出习题12-4 图所示体系的运动方程。12-5 求习题 12-5 图所示单自由度体系的自振频率。除注明者外EI=常数。 k1为弹性支座的刚度系数。12-6求习题 12-6 图所示体系的自振频率。除杆件AB 外,其余杆件为刚性杆。12-7 求习题 12-7 图所示体系的自振周期。No.12-185 第 12 章结构的动力计算12-8 某单质点单自由度体系由初位移y0=2cm 产生自由振动,经过8 个周期后测得振幅为0.2cm,试求阻尼比及在质点上作用简谐荷载发生共振时的动力系数。12-9 求习题 12-9 图所示梁纯强迫振动时的最大动力弯矩图和质点的振幅。已知:质点的重量W=24.5kN ,F P=10kN ,=52.3 s— 1,EI=3.2×107N· m2。不计梁的重量和阻尼。12-10 求习题 12-10 图所示刚架稳态振动时的最大动力弯矩图和质点的振幅。已知: FP=2.5kN ,34,EI=2.8×104kN· m2。不考虑阻尼。12-11习题 12-7(5...