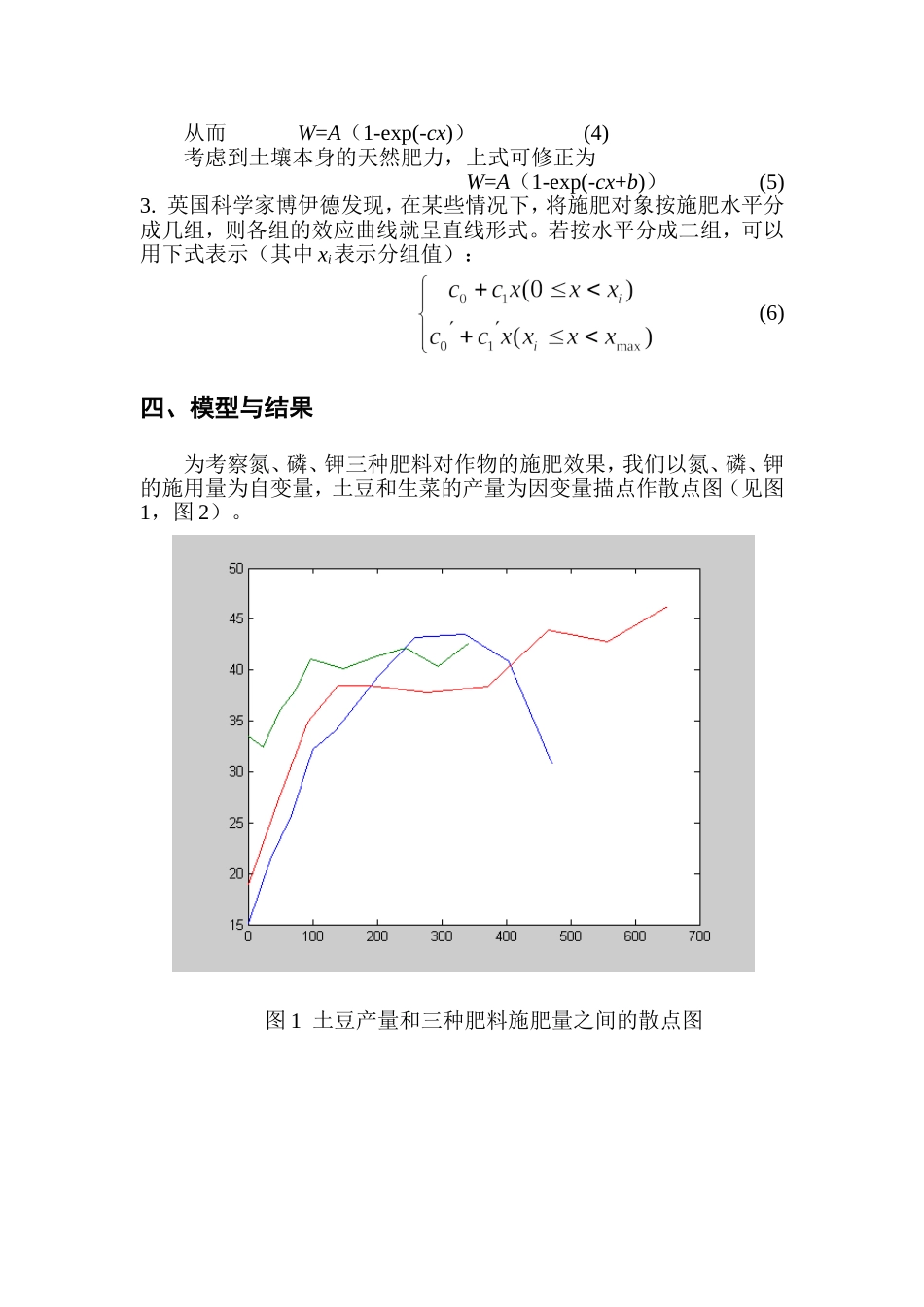
农作物施肥效果分析(1992年A题)某研究所为了研究N、P、K三种肥料对于土豆和生菜的作用,分别对每种作物进行了三组实验,实验中将每种肥料的施用量分为10个水平,在考察其中一种肥料的施用量与产量关系时,总是将另二种肥料固定在第7个水平上,实验数据如下列表格所示,其中ha表示公顷,t表示吨,kg表示千克,试建立反映施肥量与产量关系的模型,并从应用价值和如何改进等方面作出评价.施肥量与产量关系的实验数据土豆:NPK施肥量(kg/ha)产量(t/ha)施肥量(kg/ha)产量(t/ha)施肥量(kg/ha)产量(t/ha)015.18033.46018.983421.362432.474727.356725.724936.069334.8610132.297337.9614038.5213534.039841.0418638.4420239.4514740.0927937.7325943.1519641.2637238.4333643.4624542.1746543.8740440.8329440.3655842.7747130.7534242.7365146.22生菜NPK施肥量(kg/ha)产量(t/ha)施肥量(kg/ha)产量(t/ha)施肥量(kg/ha)产量(t/ha)011.0206.39015.752812.70499.484716.765614.569812.469316.898416.2714714.3814016.2411217.7519617.1018617.5616822.5929421.9427919.2022421.6339122.6437217.9728019.3448921.3446515.8433616.1258722.0755820.1139214.1168524.5365119.40一、符号说明:W:农作物产量.x:施肥量.N、P、K:氮、磷、钾肥的施用量.CW:农产品价格.CN,CP,CK:氮、磷、钾肥的价格.a,b,b0,b1,b2,c,c0,c1,c’0,c’1:常数(对特定肥料,特定农作物而言)二、模型假设1.研究所的实验是在相同的正常实验条件(如充足的水分供应,正确的耕作程序)下进行的,产量的变化是由施肥量的改变引起的,产量与施肥量之间满足一定的规律。在实验中,除施肥量,其它影响因子(如环境条件、种植密度等)均处于同等水平。2.土壤本身已含有一定数量的氮、磷、钾肥,即具有一定的天然肥力(从数据可以看出,当各种养分的施肥量都为0时,产量并不为0)。3.每次实验是独立进行的,且对于N、P、K施用量来说无系统误差,模型的误差项均服从同分布的正态分布。三、问题分析题目要求建立反映施肥量与产量关系的模型,显然这是一个回归分析的问题,但是什么样的回归模型能体现施肥量与产量之间的关系呢?这就需要从问题的实际背景出发来考察。一元回归分析理论(1-17页)及其实现(25-30页)农学规律表明,施肥量与产量一般满足这样的关系:它分成三个不同的区段,在第一区段,当施肥量比较小时,作物产量随施肥量的增加而迅速增加,第二区段,随着施肥量的增加,作物产量平缓上升,第三区段,施肥量超过一定限度后,产量反而随施肥量的增加而下降在长期的实践中,农学家们已经总结出关于作物施肥效果的经验规律,并建立了相应的理论1.Nicklas和Miller理论:设h为达到最高产量时的施肥量,边际产量(即产量W对施肥量x的导数)dW/dx与(h-x)成正比例关系,即dW/dx=a(h-x)(1)从而W=b0+b1x+b2x2(2)2.米采利希学说:只增加某种养分时,引起产量的增加与该种养分供应充足时达到的最高产量A与现在产量W之差成正比,即dW/dx=c(A-W)(3)从而W=A(1-exp(-cx))(4)考虑到土壤本身的天然肥力,上式可修正为W=A(1-exp(-cx+b))(5)3.英国科学家博伊德发现,在某些情况下,将施肥对象按施肥水平分成几组,则各组的效应曲线就呈直线形式。若按水平分成二组,可以用下式表示(其中xi表示分组值):(6)四、模型与结果为考察氮、磷、钾三种肥料对作物的施肥效果,我们以氮、磷、钾的施用量为自变量,土豆和生菜的产量为因变量描点作散点图(见图1,图2)。图1土豆产量和三种肥料施肥量之间的散点图图2生菜产量和三种肥料施肥量之间的散点图从图中看出,氮肥对于作物产量的贡献大致呈多项式关系,磷肥对于作物产量的关系大致为分段直线形式,至于钾肥,对土豆而言,大致呈指数关系。对生菜而言,随着施用量的增加,产量的上升幅度很小.这样,我们得到了对施肥效果的定性认识。我们建立了一元肥料效应回归模型,并在回归分析之前,用Chauvenent准则进行修正,剔除异常值.根据对问题的初步分析,氮肥的施肥效果应满足Nicklas和Miller理论所描述的关系,运用二次多项式回归,得到氮肥对土豆的回归方程:W=14.74+0.197N-0.00034N...