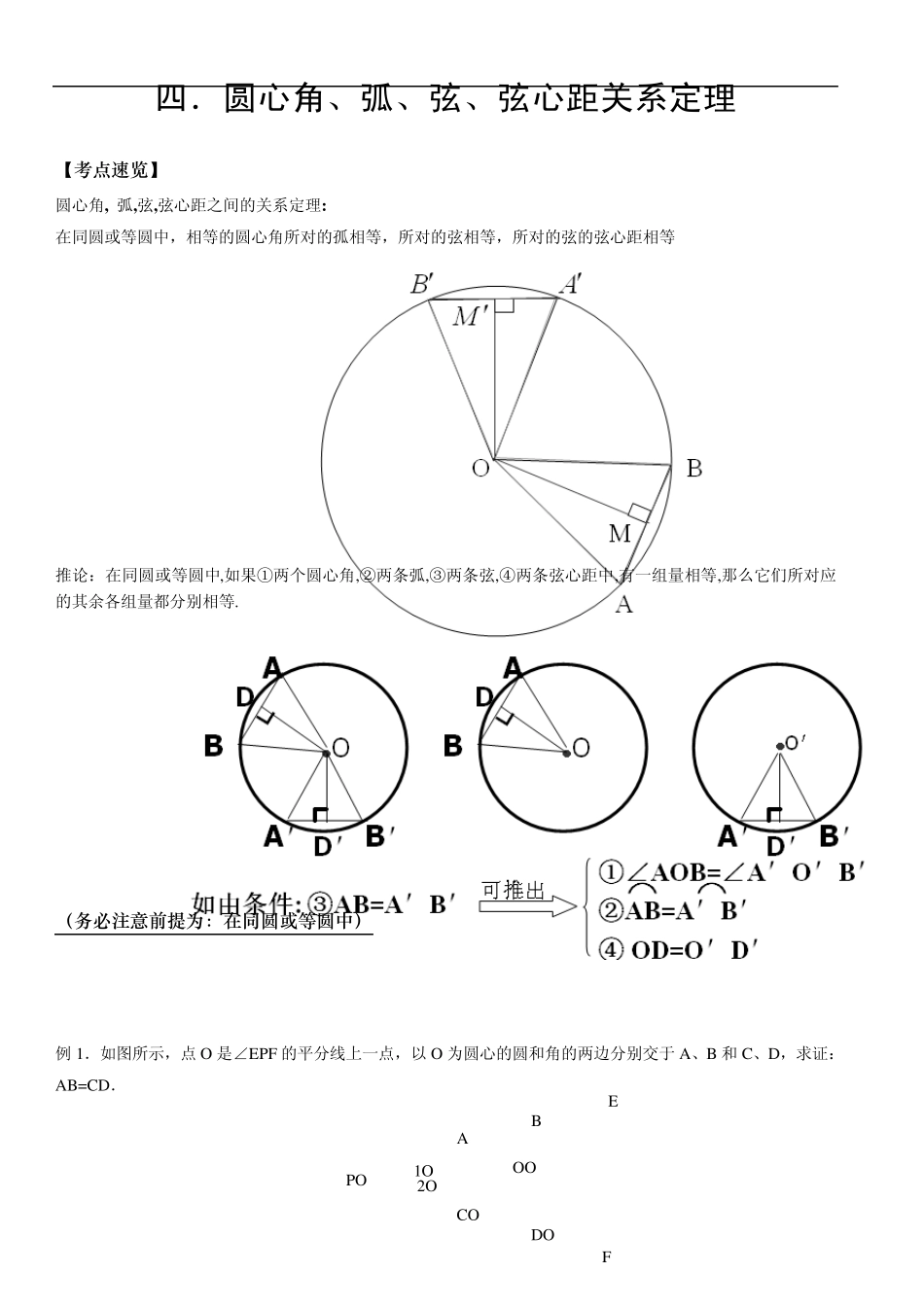
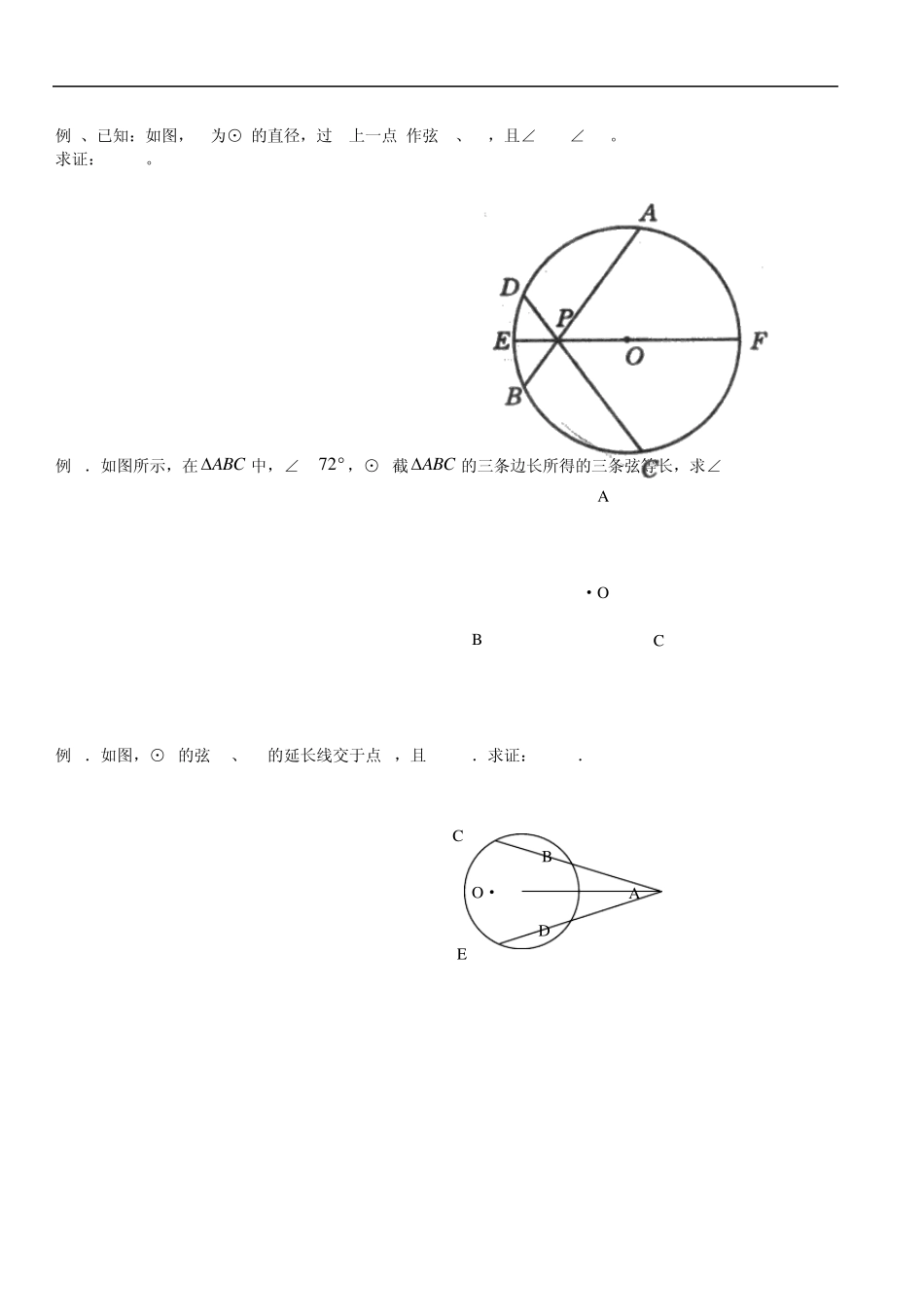
四.圆心角、弧、弦、弦心距关系定理 【考点速览】 圆心角, 弧,弦,弦心距之间的关系定理: 在同圆或等圆中,相等的圆心角所对的孤相等,所对的弦相等,所对的弦的弦心距相等 推论:在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等. (务必注意前提为:在同圆或等圆中) 例1.如图所示,点O 是∠EPF 的平分线上一点,以 O 为圆心的圆和角的两边分别交于 A、B 和 C、D,求证:AB=CD. A B E F OO PO CO 1O 2O DO 例2、已知:如图,EF为⊙O的直径,过EF上一点P作弦AB、CD,且∠APF=∠CPF。 求证:PA=PC。 例3.如图所示,在ABC中,∠A= 72 ,⊙O截ABC的三条边长所得的三条弦等长,求∠BOC. 例4.如图,⊙O的弦CB、ED的延长线交于点A,且BC=DE.求证:AC=AE. ·O A B C O· C A E B D 例5.如图所示,已知在⊙O中,弦AB=CB,∠ABC=120 ,OD⊥AB于D,OE⊥BC于E. 求证:ODE是等边三角形. 综合练习 一、选择题 1.下列说法中正确的是( ) A、相等的圆心角所对的弧相等 B、相等的弧所对的圆心角相等 C、相等的弦所对的弦心距相等 D、弦心距相等,则弦相等 2.如图,在⊙O中,AB的度数是50 ,∠OBC=40 ,那么∠OAC等于( ) A、15 B、20 C、25 D、30 3.P为⊙O内一点,已知OP=1cm,⊙O的半径r=2cm,则过P点弦中,最短的弦长为( ) A、1cm B、3 cm C、32cm D、4cm 4.在⊙O中,AB与CD为两平行弦,ABCD,AB、CD所对圆心角分别为 60,120,若⊙O的半径为6,则AB、CD两弦相距( ) A、3 B、6 C、13 D、333 5.如图所示,已知△ABC是等边三角形,以BC为直径的⊙O分别交AB、AC于点D、E。 · O 图 A B C · O A D E B C ABCODE(1)试说明△ODE的形状; (2)如图2,若∠A=60º,AB≠AC,则①的结论是否仍然成立,说明你的理由。 6 如图,△ABC是等边三角形,⊙O过点B,C,且与BA、CA的延长线分别交于点D、E.弦DF∥AC,EF的延长线交BC的延长线于点G. (1)求证:△BEF是等边三角形; (2)BA=4,CG=2,求BF的长. 7 已知:如图,∠AO B=90°,C、D是弧AB的三等分点,AB分别交O C、O D于点E、F。求证:AE=BF=CD。 ABCODE· 如图3 如图4 如图5 【作业】日期 姓名 完成时间 成绩 1.如图1,ABC内接于⊙O ,445,ABC则⊙O 的半径...