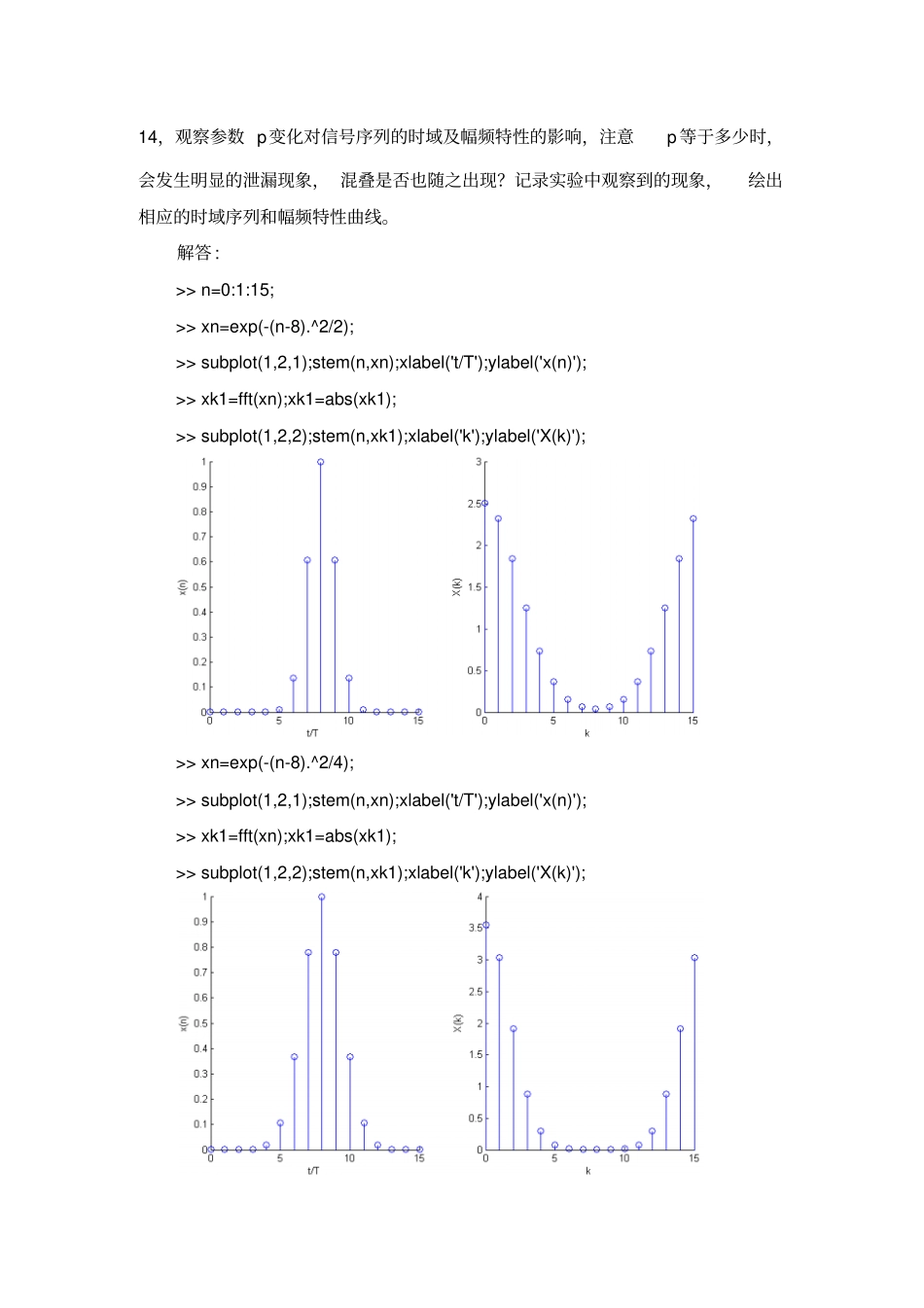
《数字信号处理》课程(2010-2011 学年第 1 学期)成绩:实验二快速傅里叶变换(FFT)及其应用学生姓名:闫春遐所在院系:电子信息工程学院自动化系年级专业: 2008 级自动化系学号:00824049 指导教师:王亮完成日期: 2010 年 9 月 27 日实验二快速傅里叶变换(FFT)及其应用一、实验目的(1)在理论学习的基础上,通过本实验,加深对FFT的理解,熟悉 MATLAB中的有关函数。(2)应用 FFT对典型信号进行频谱分析。(3)了解应用 FFT进行信号频谱分析过程可能出现的问题,以便在实际中正确应用 FFT。(4)应用 FFT实现序列的线性卷积和相关。二、实验内容实验中用到的信号序列:a)高斯序列2()015( )0npqaenx n其他b)衰减正弦序列sin(2)015( )0anbefnnx n其他c)三角波序列03( )8470cnnx nnn其他d)反三角波序列403( )4470dnnxnnn其他上机实验内容:(1)观察高斯序列的时域和幅频特性,固定信号( )ax n 中参数8p,改变 q的值,使 q 分别等于 2、4、8,观察他们的时域和幅频特性,了解当q 取不同值时,对信号的时域和幅频特性的影响;固定8q,改变 p ,使 p 分别等于 8、13、14,观察参数 p变化对信号序列的时域及幅频特性的影响,注意p 等于多少时,会发生明显的泄漏现象, 混叠是否也随之出现?记录实验中观察到的现象,绘出相应的时域序列和幅频特性曲线。解答 : >> n=0:1:15; >> xn=exp(-(n-8).^2/2); >> subplot(1,2,1);stem(n,xn);xlabel('t/T');ylabel('x(n)'); >> xk1=fft(xn);xk1=abs(xk1); >> subplot(1,2,2);stem(n,xk1);xlabel('k');ylabel('X(k)'); >> xn=exp(-(n-8).^2/4); >> subplot(1,2,1);stem(n,xn);xlabel('t/T');ylabel('x(n)'); >> xk1=fft(xn);xk1=abs(xk1); >> subplot(1,2,2);stem(n,xk1);xlabel('k');ylabel('X(k)'); >> xn=exp(-(n-8).^2/8); >> subplot(1,2,1);stem(n,xn);xlabel('t/T');ylabel('x(n)'); >> xk1=fft(xn);xk1=abs(xk1); >> subplot(1,2,2);stem(n,xk1);xlabel('k');ylabel('X(k)'); >> xn=exp(-(n-13).^2/8); >> subplot(1,2,1);stem(n,xn);xlabel('t/T');ylabel('x(n)'); >> xk1=fft(xn);xk1=abs(xk1); >> subplot(1,2,2);stem(n,xk1);xlabel('k');ylabel('X(k)'); >> xn=exp(-(n-14).^2/8); >> subplot(1,2,1);stem(n,xn);xlabel('t/T');ylabel('x(n)'); >> xk1=fft(xn);xk1=abs(xk1); >> subplot(1,2,2);stem...