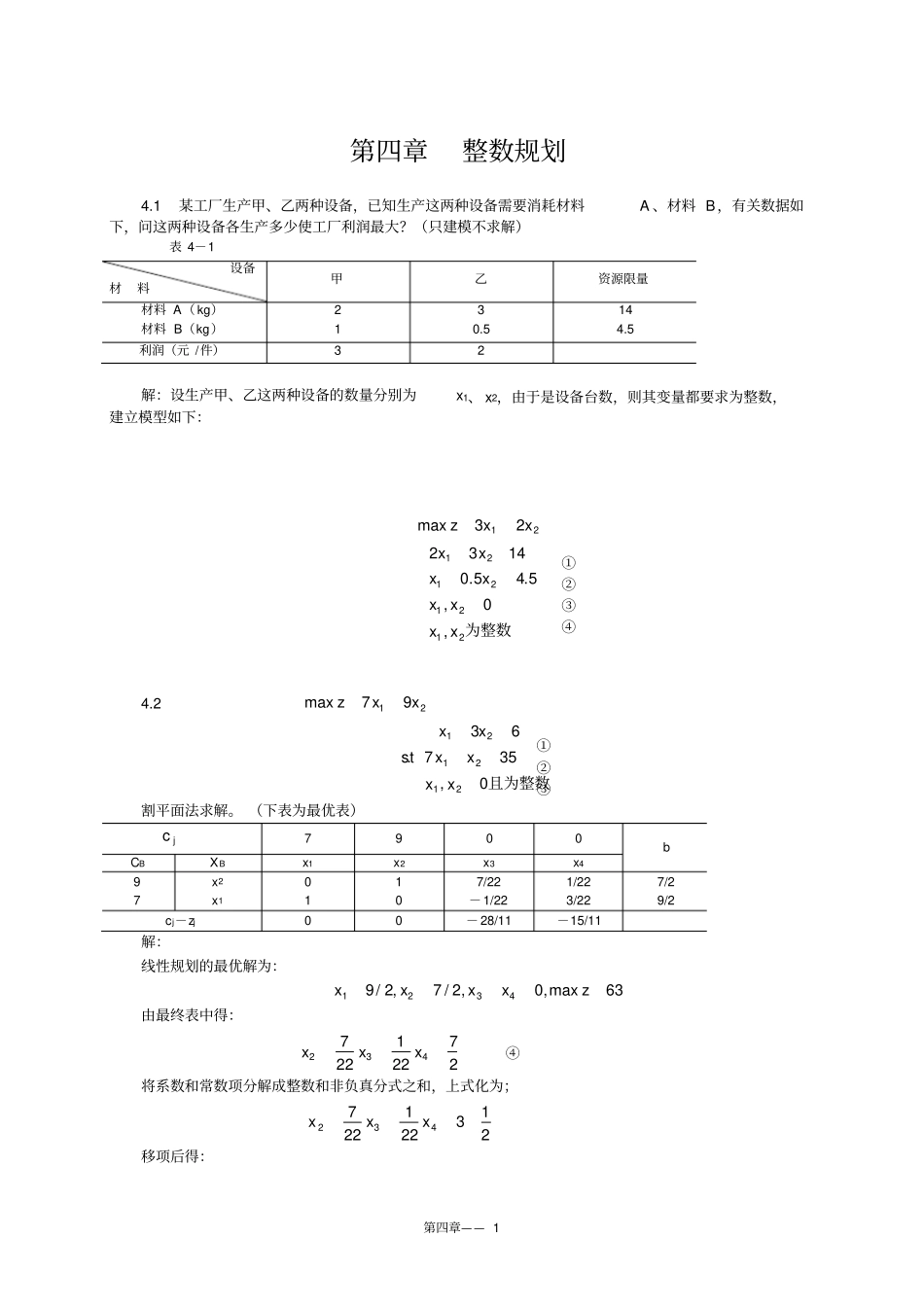
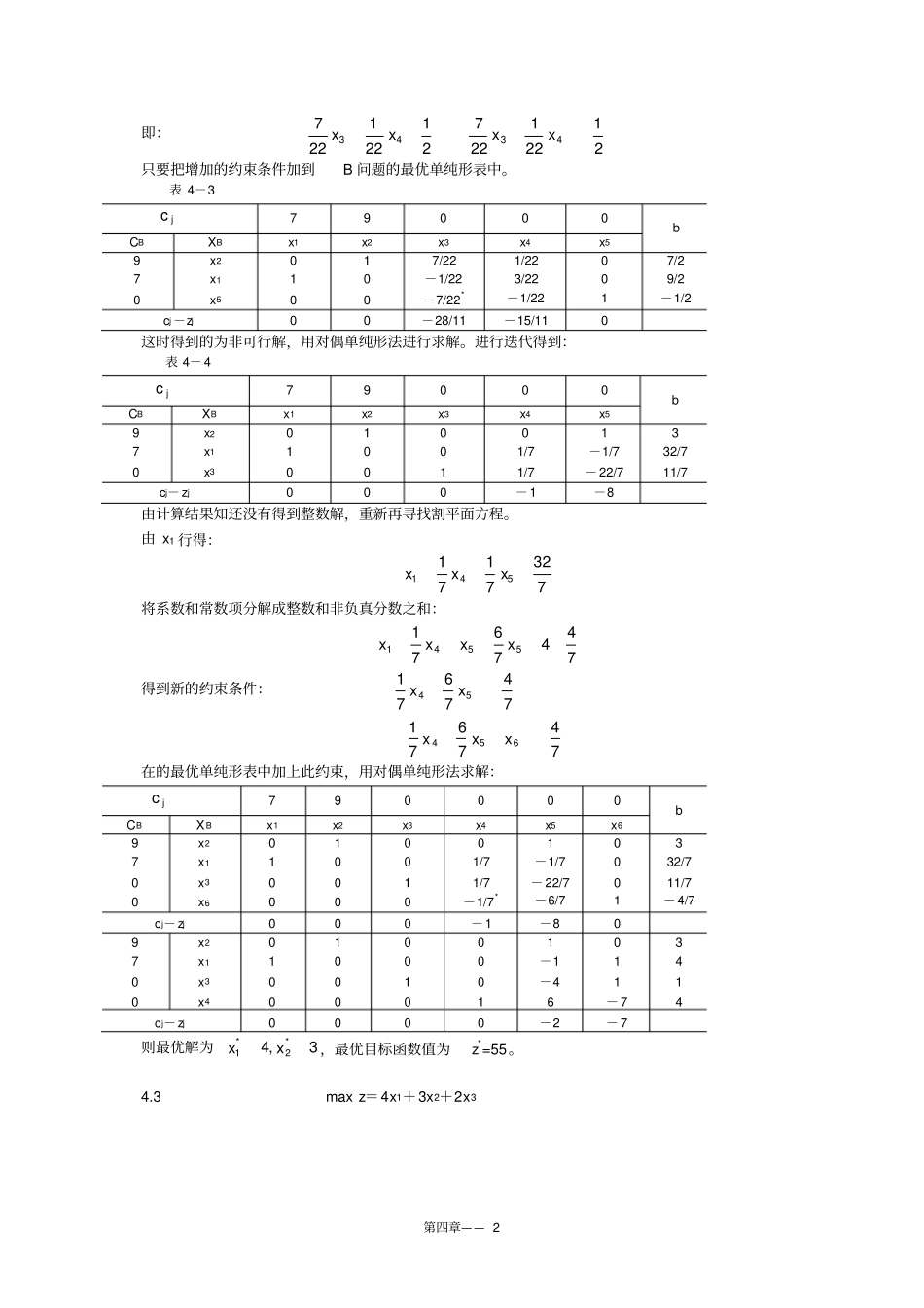
第四章—— 1 第四章整数规划4.1某工厂生产甲、乙两种设备,已知生产这两种设备需要消耗材料A 、材料 B,有关数据如下,问这两种设备各生产多少使工厂利润最大?(只建模不求解)表 4-1 设备材料甲乙资源限量材料 A( kg)2 3 14 材料 B(kg)1 0.5 4.5 利润(元 /件)3 2 解:设生产甲、乙这两种设备的数量分别为x1、 x2,由于是设备台数,则其变量都要求为整数,建立模型如下:2123maxxxz为整数21212121,0,5.45.01432xxxxxxxx4.2 2197maxxxz且为整数0,35763.212121xxxxxxts割平面法求解。 (下表为最优表)jc7 9 0 0 b CB XBx1 x2 x3x4 9 x20 1 7/22 1/22 7/2 7 x11 0 - 1/22 3/22 9/2 cj-zj 0 0 - 28/11 -15/11 解:线性规划的最优解为:63max,0,2/7,2/94321zxxxx由最终表中得:27221227432xxx④将系数和常数项分解成整数和非负真分式之和,上式化为;213221227432xxx移项后得:①②③④①②③第四章—— 2 即:21221227212212274343xxxx只要把增加的约束条件加到B 问题的最优单纯形表中。表 4-3 jc7 9 0 0 0 b CB XBx1 x2x3x4x59 x20 1 7/22 1/22 0 7/2 7 x11 0 -1/22 3/22 0 9/2 0 x50 0 -7/22* -1/22 1 -1/2 cj -zj 0 0 -28/11 -15/11 0 这时得到的为非可行解,用对偶单纯形法进行求解。进行迭代得到:表 4- 4 jc7 9 0 0 0 b CB XBx1 x2x3x4x59 x20 1 0 0 1 3 7 x11 0 0 1/7 -1/7 32/7 0 x30 0 1 1/7 - 22/7 11/7 cj- zj 0 0 0 - 1 -8 由计算结果知还没有得到整数解,重新再寻找割平面方程。由 x1 行得:7327171541xxx将系数和常数项分解成整数和非负真分数之和:74476715541xxxx得到新的约束条件:74767154xx747671654xxx在的最优单纯形表中加上此约束,用对偶单纯形法求解:jc7 9 0 0 0 0 b CB XBx1 x2x3x4x5 x6 9 x20 1 0 0 1 0 3 7 x11 0 0 1/7 -1/7 0 32/7 0 x30 0 1 1/7 - 22/7 0 11/7 0 x60 0 0 -1/7* -6/7 1 - 4/7 cj- zj 0 0 0 - 1 -8 0 9 x20 1 0 0 1 0 3 7 x11 0 0 0 -1 1 4 0 x30 0 1 0 -4 1 1 0 x40 0 0 1 6 - 7 4 cj- zj 0 0 0 0 -2 - 7 则最优解为3,4*2*1xx,最优目标函数值为z*=55。4.3 max z=4x1+3x2+2x3第四章—— 3 10,,13344352.32...