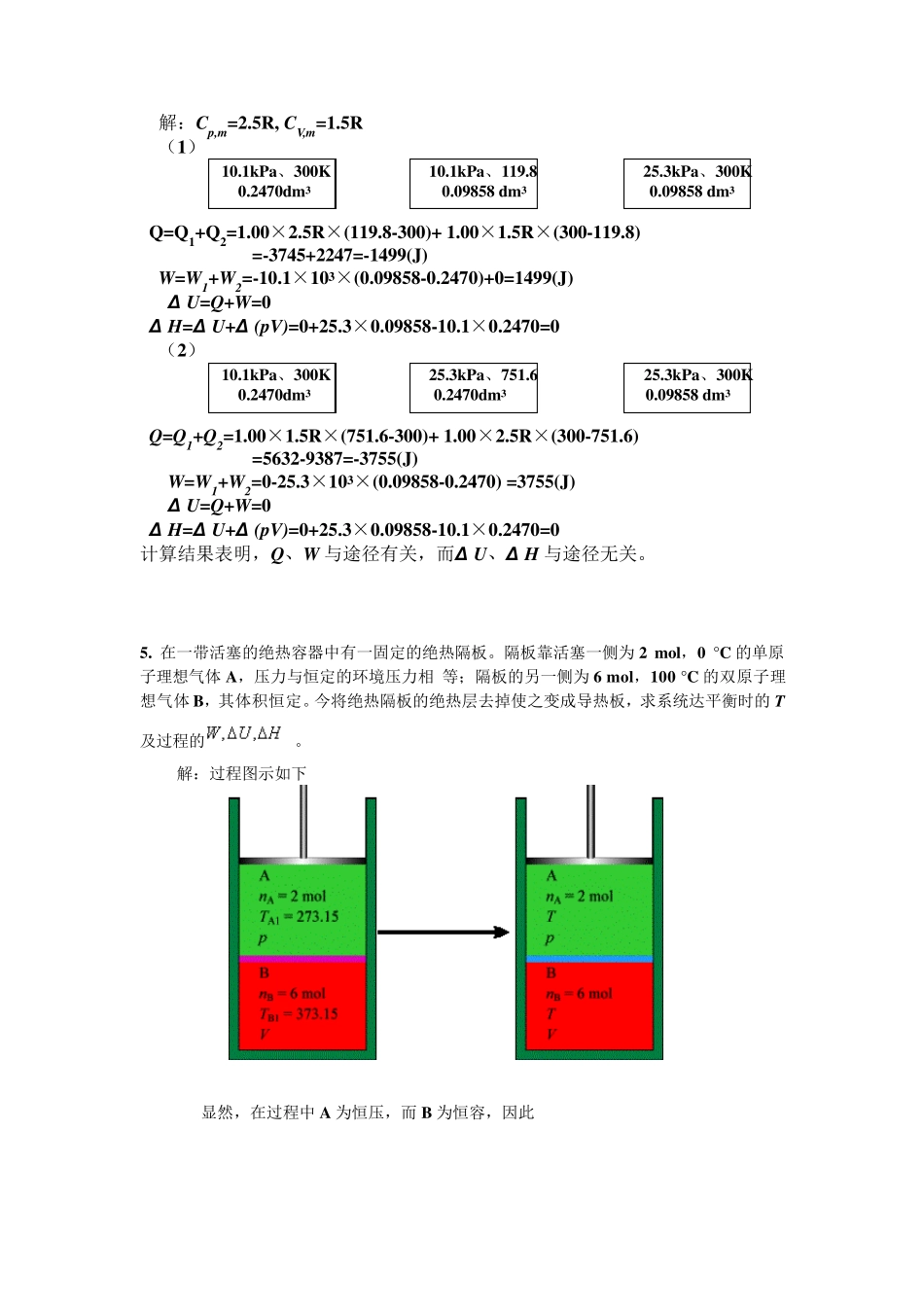
第二章 热力学第一定律 1. 始态为25 °C,200 kPa 的5 mol 某理想气体,经途径a,b 两不同途径到达相同的末态。途经a 先经绝热膨胀到 -28.47 °C,100 kPa,步骤的功;再恒容加热到压力200 kPa 的末态,步骤的热。途径b 为恒压加热过程。求途径b 的及。 解:先确定系统的始、末态 对于途径b,其功为 根据热力学第一定律 2. 2 mol 某理想气体,。由始态100 kPa,50 dm3,先恒容加热使压力体积增大到150 dm3,再恒压冷却使体积缩小至 25 dm3。求整个过程的 。 解:过程图示如下 由于,则,对有理想气体和只是温度的函数 该途径只涉及恒容和恒压过程,因此计算功是方便的 根据热力学第一定律 3. 单原子理想气体A 与双原子理想气体B 的混合物共5 mol,摩尔分数,始态温度,压力。今该混合气体绝热反抗恒外压膨胀到平衡态。求末态温度及过程的。 解:过程图示如下 分析:因为是绝热过程,过程热力学能的变化等于系统与环境间以功的形势所交换的能 量。因此, 单原子分子,双原子分子 由于对理想气体U 和H 均只是温度的函数,所以 4. 1.00mol(单原子分子)理想气体,由10.1kPa、300K 按下列两种不同的途径压缩到25.3kPa、300K,试计算并比较两途径的Q、W 、ΔU 及ΔH。 (1)等压冷却,然后经过等容加热; (2)等容加热,然后经过等压冷却。 解:Cp,m=2.5R, CV,m=1.5R (1) 10.1kPa、300K 10.1kPa、119.8 25.3kPa、300K 0.2470dm3 0.09858 dm3 0.09858 dm3 Q=Q1+Q2=1.00×2.5R×(119.8-300)+ 1.00×1.5R×(300-119.8) =-3745+2247=-1499(J) W=W1+W2=-10.1×103×(0.09858-0.2470)+0=1499(J) Δ U=Q+W=0 Δ H=Δ U+Δ (pV)=0+25.3×0.09858-10.1×0.2470=0 (2) 10.1kPa、300K 25.3kPa、751.6 25.3kPa、300K 0.2470dm3 0.2470dm3 0.09858 dm3 Q=Q1+Q2=1.00×1.5R×(751.6-300)+ 1.00×2.5R×(300-751.6) =5632-9387=-3755(J) W=W1+W2=0-25.3×103×(0.09858-0.2470) =3755(J) Δ U=Q+W=0 Δ H=Δ U+Δ (pV)=0+25.3×0.09858-10.1×0.2470=0 计算结果表明,Q、W 与途径有关,而Δ U、Δ H 与途径无关。 5. 在一带活塞的绝热容器中有一固定的绝热隔板。隔板靠活塞一侧为 2 mol,0 °C 的单原子理想气体 A,压力与恒定的环境压力相 等;隔板的另一侧为 6 mol,100 °C 的双原子理想气体 B,其体积恒定。今将绝热隔板的绝热层去掉使之变...