现代信号处理例题及matlab代码实现

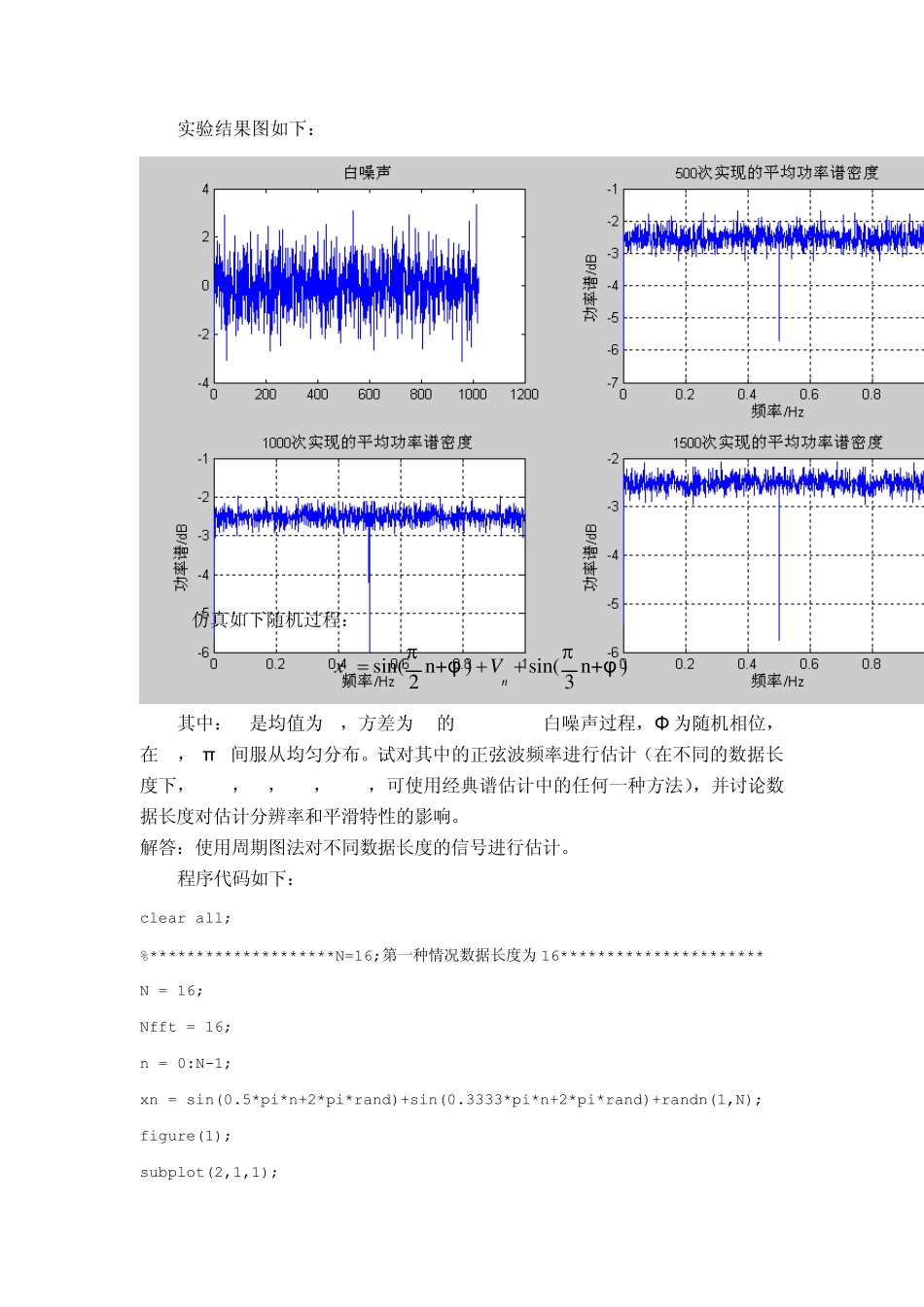
《现代信号处理》期末考核作业 1 MATLAB仿真均值为0，方差为1的白噪声信号，信号长度N=1024，并用周期图法分别求500、1000和 1500次实现的平均功率谱密度，画图。 程序代码如下： clear; clear all; N=1024;%数据长度 Nfft=1024;%FFT 所采用的数据长度 n=0:N-1; wn=randn(1,N);%产生随机白噪声 subplot(2,2,1);%绘出白噪声序列 plot(n,wn); title('白噪声'); %500 次实现的平均功率谱密度 s=zeros(1,N); for i=1:500 wn=randn(1,N);%产生随机白噪声 Pxx=10*log10(abs(fft(wn,Nfft).^2)/N);%Fourier 振幅谱平方的平均值，并转换为db s=s+Pxx; end s=s/500; f=(0:length(Pxx)-1)/length(Pxx);%绘出频率序列 subplot(222); plot(f,s); xlabel('频率/Hz');ylabel('功率谱/dB'); title('500 次实现的平均功率谱密度'); grid on; %1000 次实现的平均功率谱密度 s=zeros(1,N); for i=1:1000 wn=randn(1,N);%产生随机白噪声 Pxx=10*log10(abs(fft(wn,Nfft).^2)/N);%Fourier 振幅谱平方的平均值，并转换为db s=s+Pxx; end s=s/1000; f=(0:length(Pxx)-1)/length(Pxx);%绘出频率序列 subplot(223); plot(f,s); xlabel('频率/Hz');ylabel('功率谱/dB'); title('1000 次实现的平均功率谱密度'); grid on; %500 次实现的平均功率谱密度 s=zeros(1,N); for i=1:1500 wn=randn(1,N);%产生随机白噪声 Pxx=10*log10(abs(fft(wn,Nfft).^2)/N);%Fourier 振幅谱平方的平均值，并转换为db s=s+Pxx; end s=s/1500; f=(0:length(Pxx)-1)/length(Pxx);%绘出频率序列 subplot(224); plot(f,s); xlabel('频率/Hz');ylabel('功率谱/dB'); title('1500 次实现的平均功率谱密度'); grid on; 实验结果图如下： 2仿真如下随机过程： sin(n+)sin(n+)23nnxVφφ 其中：Vn是均值为0，方差为1的Gaussian白噪声过程，Φ 为随机相位，在[0，2π ]间服从均匀分布。试对其中的正弦波频率进行估计（在不同的数据长度下，N=16，64，128，1024，可使用经典谱估计中的任何一种方法），并讨论数据长度对估计分辨率和平滑特性的影响。 解答：使用周期图法对不同数据长度的信号进行估计。 程序代码如下： clear all; %********************N=16;第一种情况数据长度为16********************** N = 16; Nfft = 16; n = 0:N-1; xn = sin(0.5*pi*n+2*pi*rand)+sin(0.3333*pi*n+2*pi*rand)...