现代测试技术习题例题

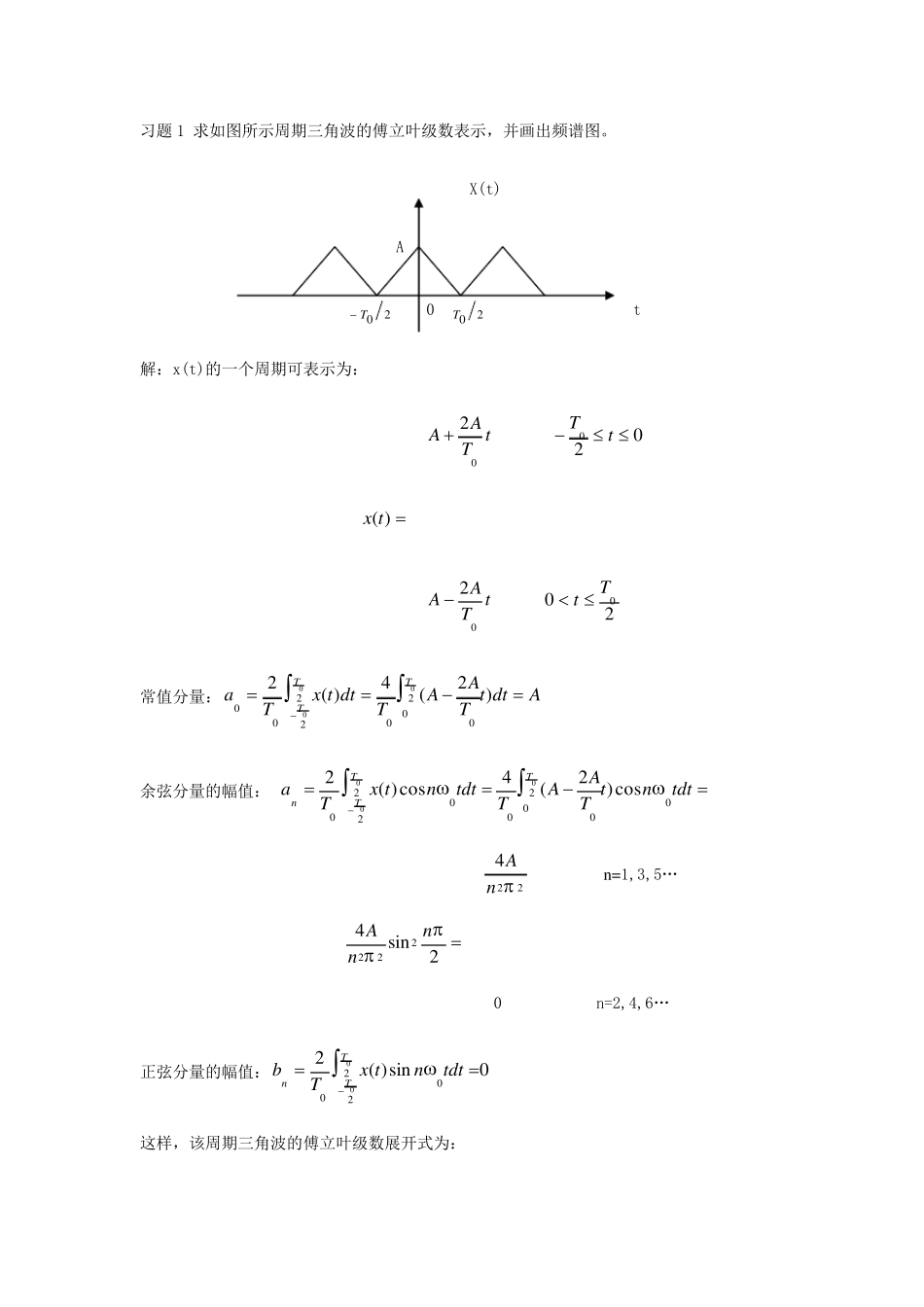
习题1 求如图所示周期三角波的傅立叶级数表示，并画出频谱图。 X(t) A 20T 0 20T t 解：x(t)的一个周期可表示为： tTAA02 020tT )(tx tTAA02 200Tt  常值分量：AdttTAATdttxTaTTT)2(4)(220022000000 余弦分量的幅值： tdtntTAATtdtntxTaTTTn020022000cos)2(4cos)(2000 224nA n=1,3,5… 2sin4222nnA 0 n=2,4,6… 正弦分量的幅值：0sin)(2220000TTntdtntxTb 这样，该周期三角波的傅立叶级数展开式为： tnnAAtttAAtxn0122020202cos1425cos513cos31cos42)( nA n 0 30 50  0 30 50 练习2 求指数衰减振荡信号tetxat0sin)(的频谱函数。 解一： 202000)()(000)(00)(121)(1)(1221][221)()(2sinsin21sin21)(0000jajjajjajdteejXeejttdtedtteeXtjjatjjatjtjtjatjat 解二：)()(22sin000ffffjtf fjae at21 )()()(TtxTttx )()()()(fYfXtytx• 000002)2(12)2(12)()(2212sinfjfjafjfjajffffjfjatfe at 4. 求指数衰减函数 的频谱函数 ，（ ）。并定性画出信号及其频谱图形。 解：（1）求单边指数函数 的傅里叶变换及频谱 （2）求余弦振荡信号 的频谱。 利用 函数的卷积特性,可求出信号 的频谱为 其幅值频谱为 a a` b b` c c` 题图 信号及其频谱图 注：本题可以用定义求，也可以用傅立叶变换的频移特性求解。 练习 3 已知信号x(t)的傅立叶变换为X(f),求tftxtf02cos)()(的傅立叶变换。 解一：dtetxFtj)(21)( )()(21)()(41)(21)(21cos)(2100)()(000XXdtetxdtetxdteeetxdttetxtjtjtjtjtjtj 解二： 2/)()(2cos000fffftf 且 )()()(TtxTttx 2/)(2/)(2/)()()(2cos)(00000ffXffXfffffXtftx 1 求周期方波的傅立叶级数（复指数函数形式），画出|cn|- 和-图。 解：(1)方波的时域描述为： (...