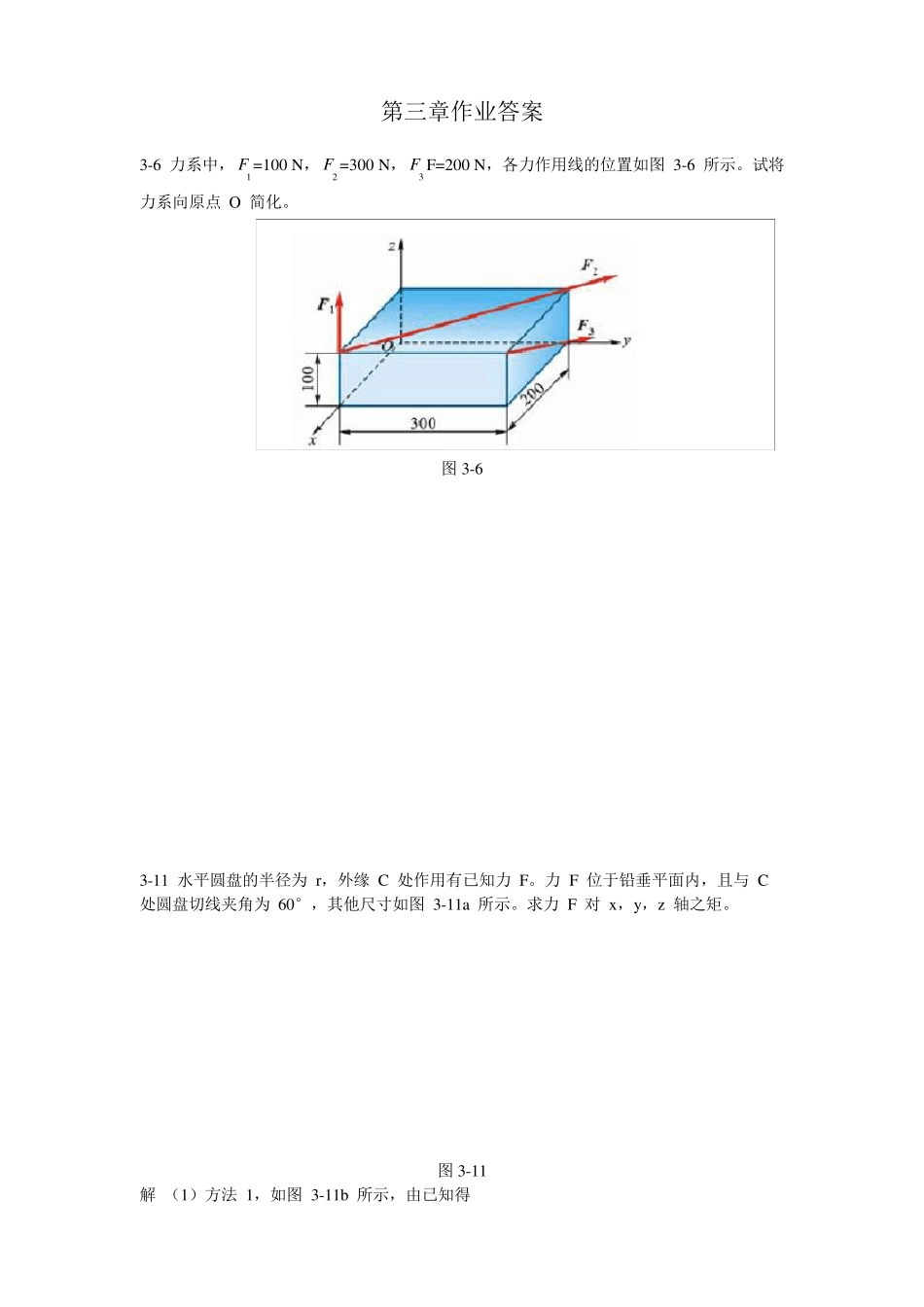
第三章作业答案 3-6 力系中,1F =100 N,2F =300 N,3F F=200 N,各力作用线的位置如图 3-6 所示。试将力系向原点 O 简化。 图3-6 3-11 水平圆盘的半径为 r,外缘 C 处作用有已知力 F。力 F 位于铅垂平面内,且与 C 处圆盘切线夹角为 60°,其他尺寸如图 3-11a 所示。求力 F 对 x,y,z 轴之矩。 图3-11 解 (1)方法 1,如图 3-11b 所示,由已知得 (2)方法 2 3-14 图 3-14a 所示空间桁架由杆 1,2,3,4,5 和 6 构成。在节点 A 上作用 1 个力 F, 此力在矩形 ABDC 平面内,且与铅直线成 45°角。 Δ EAK =ΔFBM。等腰三角形 EAK,FBM 和 NDB 在顶点 A,B 和 D 处均为直角,又 EC=CK=FD=DM。若 F=10 kN,求各杆的内力。 图3-14 解 (1) 节点 A 为研究对象,受力及坐标如图 3-14b 所示 (2)节点 B 为研究对象,受力如图 3-14b 所示 3-19 图 3-19a 所示 6 杆支撑 1 水平板,在板角处受铅直力 F 作用。设板和杆自重不计, 求各杆的内力。 图3-19 解 截开 6 根杆,取有板的部分为研究对象,受力如图 3-19b 所示。 3-22 杆系由球铰连接,位于正方体的边和对角线上,如图 3-22a 所示。在节点 D 沿对 角线 LD 方向作用力DF 。在节点 C 沿 CH 边铅直向下作用 F。如球铰 B,L 和 H 是固定的,杆重不计,求各杆的内力。 图3-22 解 (1)节点 D 为研究对象,受力如图 3-22b 所示 (2)节点 C 为研究对象,受力如图 3-22b 所示 3-25 工字钢截面尺寸如图 3-25a 所示,求此截面的几何中心。 图3-25 解 把图形的对称轴作轴 x,如图 3-25b 所示,图形的形心 C 在对称轴 x 上,即 第五章作业答案 5-3 如图 5-3 所示,半圆形凸轮以等速ov = 0.01m/s 沿水平方向向左运动,而使活塞杆 AB 沿铅直方向运动。当运动开始时,活塞杆 A 端在凸轮的最高点上。如凸轮的半径R =80mm,求活塞上 A 端相对于地面和相对于凸轮的运动方程和速度,并作出其运动图和速度图。 图5-3 解 1)A 相对于地面运动 把直角坐标系 x Oy 固连在地面上,如图 5-3b 所示,则 A 点的运动方程为 0x , 22 2200.01 64yRv tt m (08)t A 的速度 0xvx,20.01/64ytvym st A 的运动图( y -t 曲线)及速度图(yv -t 曲线)如图 5-3b 的左部。 2)A 相对于凸轮运动...