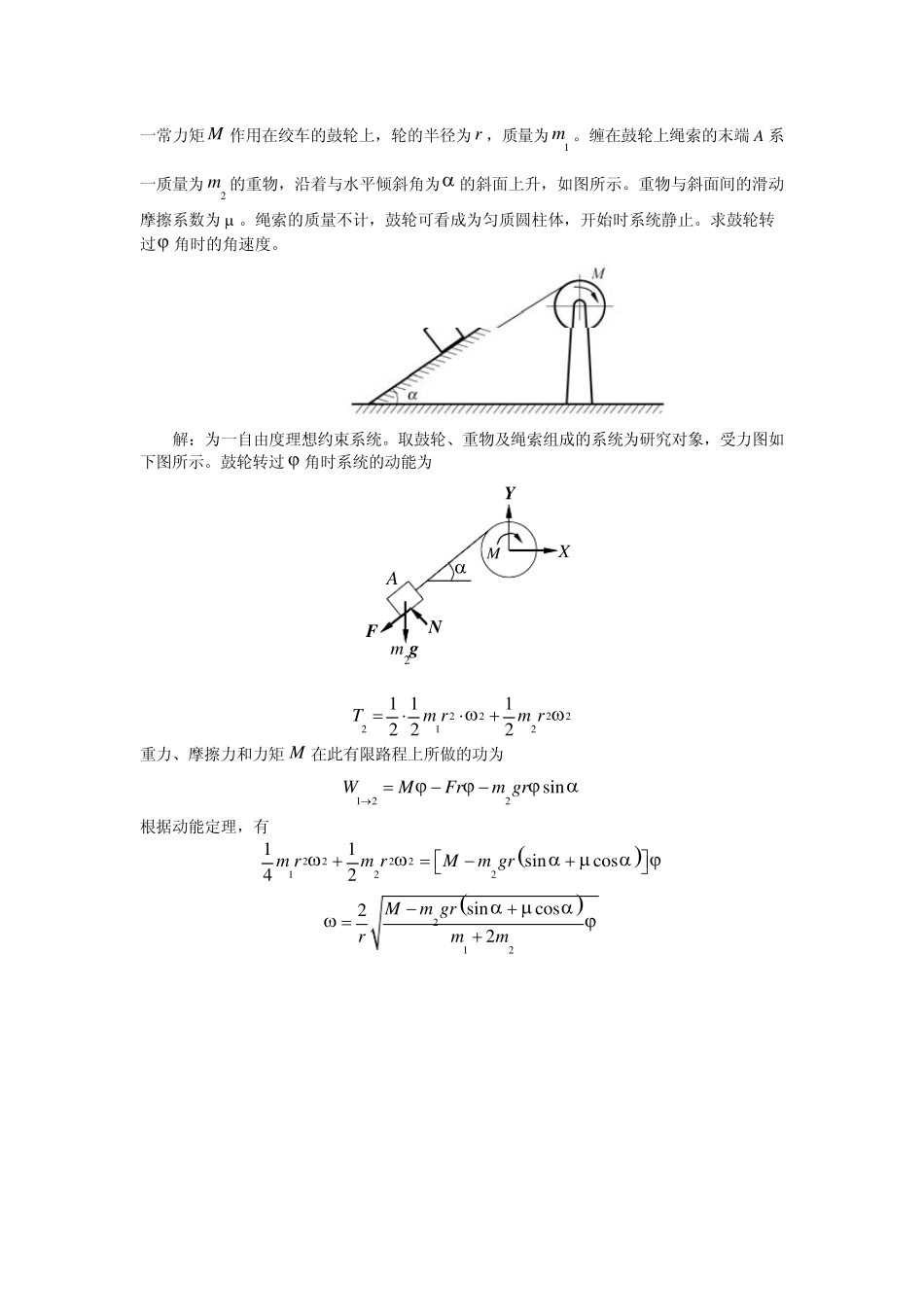
计算图示各系统的动能: (1)偏心圆盘的质量为,偏心距OCme=,对质心的回转半径为Cρ ,绕轴O 以角速度0ω转动(图a)。 (2)长为l ,质量为的匀质杆,其端部固结半径为,质量为的匀质圆盘。杆绕轴O以角速度mrm0ω 转动(图b)。 (3)滑块 A 沿水平面以速度移动,重块 B 沿滑块以相对速度下滑,已知滑块 A 的质量为,重块 B 的质量为(图c)。 1v2v1m2m(4)汽车以速度沿平直道路行驶,已知汽车的总质量为0vM ,轮子的质量为m ,半径为R ,轮子可近似视为匀质圆盘(共有 4 个轮子)(图d)。 解: (1) 222200111()222CCCTmvJm e2ωρω=+=+ (2) 2222111(83)326OJmlmrmlm lr=++=+2 220011(83)212OTJm lr 22ωω==+ (3) 22121122ABTm vm v=+ 2221 121212221212221211(2cos150 )22311()222m vm vvv vmmvm vm v v°=+++=++− (4) ()22220002111 11(4 )4222 22vTMm vmvmRMm vR⎛⎞=−+ ⋅+⋅⋅=+⎜⎟⎝⎠20 一常力矩M 作用在绞车的鼓轮上,轮的半径为r,质量为。缠在鼓轮上绳索的末端A 系一质量为的重物,沿着与水平倾斜角为1m2mα 的斜面上升,如图所示。重物与斜面间的滑动摩擦系数为μ 。绳索的质量不计,鼓轮可看成为匀质圆柱体,开始时系统静止。求鼓轮转过ϕ 角时的角速度。 解:为一自由度理想约束系统。取鼓轮、重物及绳索组成的系统为研究对象,受力图如下图所示。鼓轮转过ϕ 角时系统的动能为 αFNm2gXYMA 2222121 112 22Tm rm r2ωω=⋅⋅+ 重力、摩擦力和力矩M 在此有限路程上所做的功为 122sinWMFrm grϕϕϕ→α=−− 根据动能定理,有 ()222212211sincos42m rm rMm grωωαμ+=−+αϕ⎡⎤⎣⎦ ()212sincos22Mm grrmmαμαωϕ−+=+ 绞车提升一质量为m 的重物,如图所示。绞车在主动轴上作用一不变的转动力矩PM 。已知主动轴和从动轴连同安装在这两轴上的齿轮以及其他附属零件的转动惯量分别为和,传速比1J2J12/zzi= 。吊索缠绕在鼓轮上,鼓轮的半径为R 。设轴承的摩擦以及吊索的质量均可略去不计。试求重物的加速度。 解:为一自由度理想约束系统,取整体系统为研究对象。由运动学关系得 212,vviiRRωωω=== 系统的动能为 22222211221221111 ()2222vTJJmvJ iJmRRωω=++=++ 22122d()dvTJ iJmRR=++v 作用在系统上的力系的元功为 1dd() vWMtmgv tMimgRtdRδω=−=− 由动能定理的微分形式得 2212()MimgR RaJ iJmR−=++ 匀质圆...