反比例函数常见几何模型

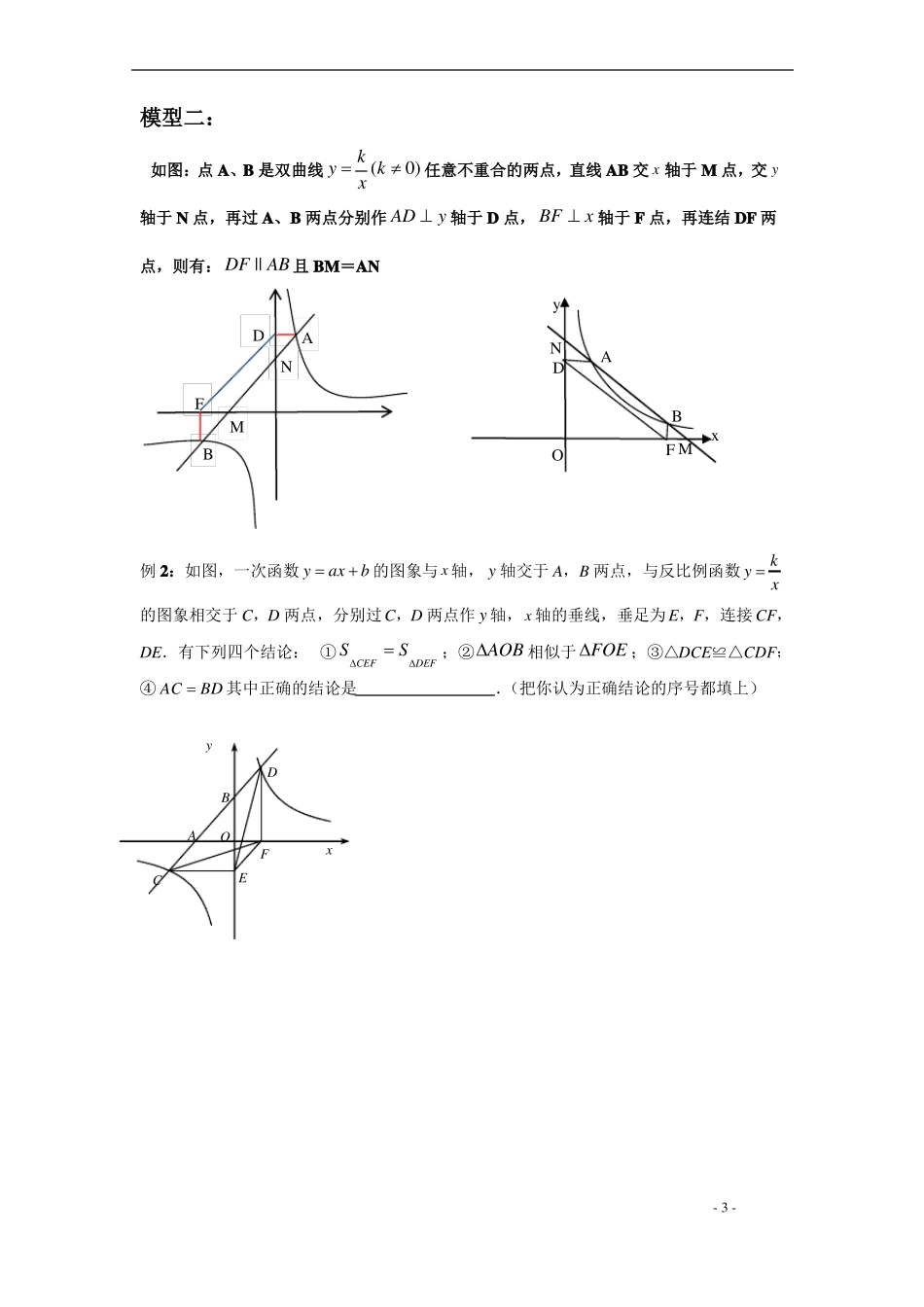
反比例函数常见模型一、知识点回顾1..反比例函数的图像是双曲线，故也称双曲线 y=（k≠0）．其解析式有三种表示方法：kxk1（k  0）；② y  kx（k  0）；③ xy  kxk2．反比例函数 y=（k≠0）的性质x① y （1）当 k>0 时 函数图像的两个分支分别在第一，三象限内 在每一象限内，y 随x 的增大而减小．（2）当 k<0 时 函数图像的两个分支分别在第二，四象限内 在每一象限内，y 随x 的增大而增大．（3）在反比例函数 y=一点横坐标与纵坐标之积).k中，其解析式变形为 xy=k，故要求 k 的值(也就是求其图像上xk图像上一点（a，b）满足 a，b 是方程 Z2－4Z－2=0 的两根，求双x2曲线的解析式．由根与系数关系得 ab=－2，又 ab=k，∴k=－2，故双曲线的解析式是 y=．x（4）若双曲线 y=（5）由于反比例函数中自变量 x 和函数 y 的值都不能为零，所以图像和 x 轴，y 轴都没有交点，但画图时要体现出图像和坐标轴无限贴近的趋势．二、新知讲解与例题训练模型一 ：如图，点 A 为反比例函数 y | k |k 图象上的任意一点，且 AB 垂直于 x 轴，则有SOAB  2xBA- 1 -例 1：如图 RtABC 的锐角顶点是直线 y=x+m 与双曲线 y= m在第一象限的交点，且xSAOB  3 ,（1）求 m 的值（2）求ABC 的面积变式题1、如图所示，点 A1, A2 , A3 在 x 轴上，且 O A1= A1A2 = A2 A3,分别过 A1, A2 , A3 作 y 轴平行线，与反比例函数 y= 8(x>0)的图像交于点 B1, B2 , B3 ，分别过点 B1, B2 , B3 作 x 轴的平行x线，分别与 y 轴交于点 C1, C2 , C3 ,连结 OB1,OB2,OB3 ,那么图中阴影部分的面积之和为__________2、 如图，点 A 在双曲线 y  13上，点 B 在双曲线 y 上，且 AB∥x 轴，C、D 在 x 轴上，xx若四边形 ABCD 为矩形，则它的面积为 .- 2 -模型二：如图：点 A、B 是双曲线 y (k  0) 任意不重合的两点，直线 AB 交 x 轴于 M 点，交 y轴于 N 点，再过 A、B 两点分别作 AD  y 轴于 D 点， BF  x 轴于 F 点，再连结 DF 两点，则有： DF || AB 且 BM＝ANkxBFMDNAyNDABOF Mx例 2：如图，一次函数 y  ax  b 的图象与 x 轴， y 轴交于 A，B 两点，与反比例函数 y  kx的图象相交于 C，D 两点，分别过 C，D 两点作 y 轴， x 轴的...