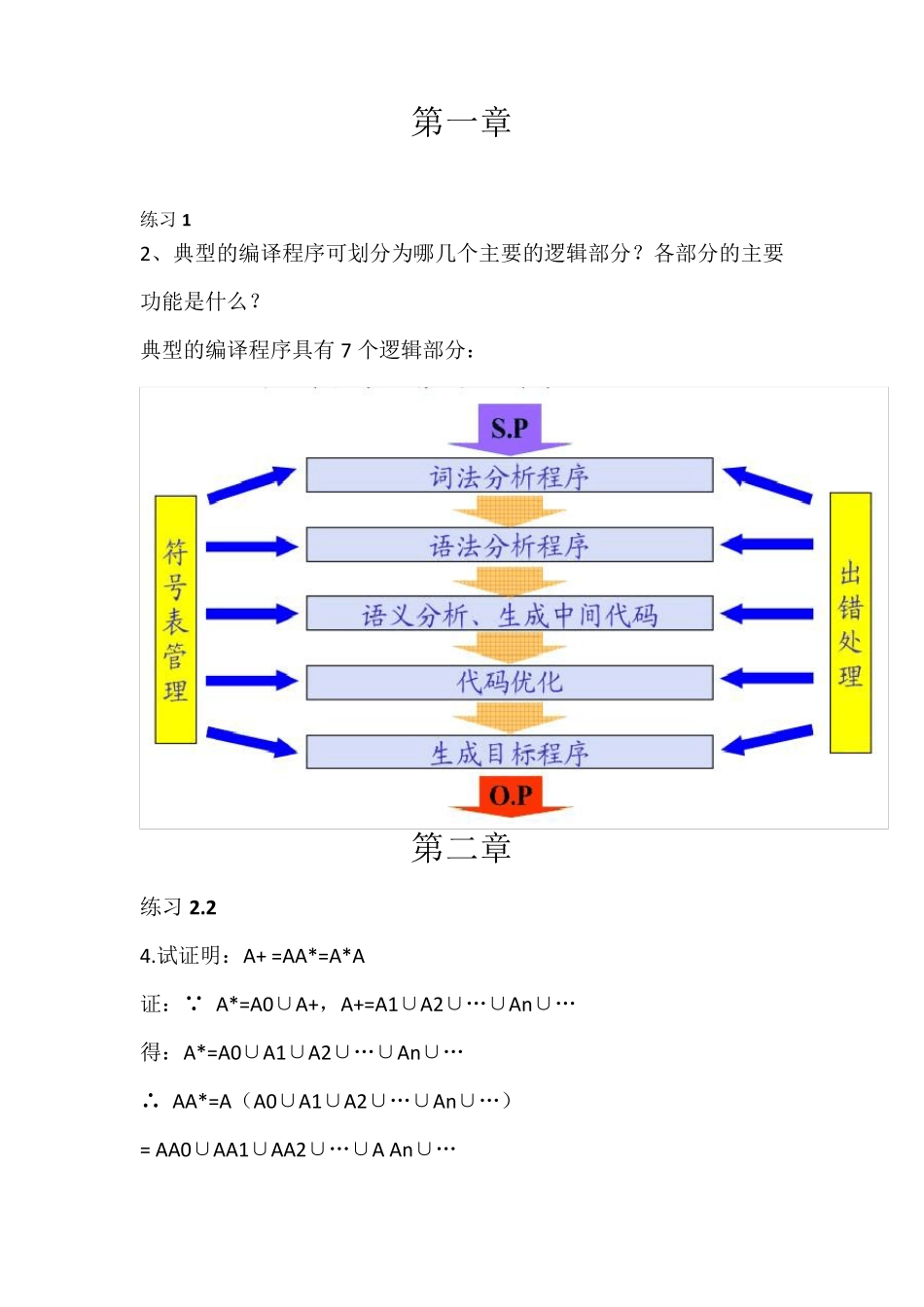
第一章 练习1 2、典型的编译程序可划分为哪几个主要的逻辑部分?各部分的主要功能是什么? 典型的编译程序具有7 个逻辑部分: 第二章 练习2.2 4.试证明:A+ =AA*=A*A 证: A*=A0∪A+,A+=A1∪A2∪…∪An∪… 得:A*=A0∪A1∪A2∪…∪An∪… ∴ AA*=A(A0∪A1∪A2∪…∪An∪…) = AA0∪AA1∪AA2∪…∪A An∪… =A∪A2∪A3∪An +1∪… = A+ 同理可得: A*A =(A0∪A1∪A2∪…∪An∪…)A =A0 A∪A1A∪A2A∪…∪AnA∪… = A∪A2∪A3∪An+1∪… = A+ 因此: A+ =AA*=A*A 练习 2.3 1.设 G[〈标识符〉]的规则是 : 〈标识符〉::=a|b|c| 〈标识符〉a|〈标识符〉c| 〈标识符〉0|〈标识符〉1 试写出 VT 和 VN, 并对下列符号串 a,ab0,a0c01,0a,11,aaa 给出可能的一些推导。 解:VT ={a,b,c,0,1}, VN ={〈标识符〉} (1) 不能推导出 ab0,11,0a (2)〈标识符〉=>a (3)〈标识符〉=>〈标识符〉1 =>〈标识符〉01 =>〈标识符〉c01 =>〈标识符〉0c01 => a0c01 (4)〈标识符〉=>〈标识符〉a =>〈标识符〉aa =>aaa 2.写一文法,其语言是偶整数的集合 解:G[<偶整数>]: <偶整数>::= <符号> <偶数字>| <符号><数字串><偶数字> <符号> ::= + | — |ε <数字串>::= <数字串><数字>|<数字> <数字> ::= <偶数字>| 1 | 3 | 5 | 7 | 9 <偶数字> ::=0 | 2 | 4 | 6 | 8 4. 设文法G 的规则是: 〈A〉::=b
| cc 试证明:cc, bcc, bbcc, bbbcc∈L[G] 证:(1)〈A〉=>cc (2)〈A〉=>b〈A〉=>bcc (3)〈A〉=>b〈A〉=>bb〈A〉=>bbcc (4)〈A〉=>b〈A〉=>bb〈A〉=>bbb〈A〉=>bbbcc 又 cc, bcc, bbcc, bbbcc∈Vt* ∴由语言定义,cc, bcc, bbcc, bbbcc∈L[G] 5 试对如下语言构造相应文法: (1){ a(bn)a | n=0,1,2,3,……},其中左右圆括号为终结符。 (2) { (an)(bn) | n=1,2,3,……} 解:(1)文法[G〈S〉]: S::= a(B)a B::= bB |ε ( 2 ) 文法[G〈S〉]:--错了,两个 n 不等 S ::= (A)(B) A::= aA|a B::= bB|b 7.对文法 G3[〈表达式〉] 〈表达式〉::=〈项〉|〈表达式〉+〈项〉|〈表达式〉-〈项〉 〈项〉::=〈因子〉|〈项〉*〈因子〉|〈项〉/〈因子〉 〈因子〉::=(〈表达式〉)| i 列出句型〈表达式〉+〈项〉*〈因子〉的所有短语和简单短语。 <表达式> => <表达式> + <项> => <表达式> + <...