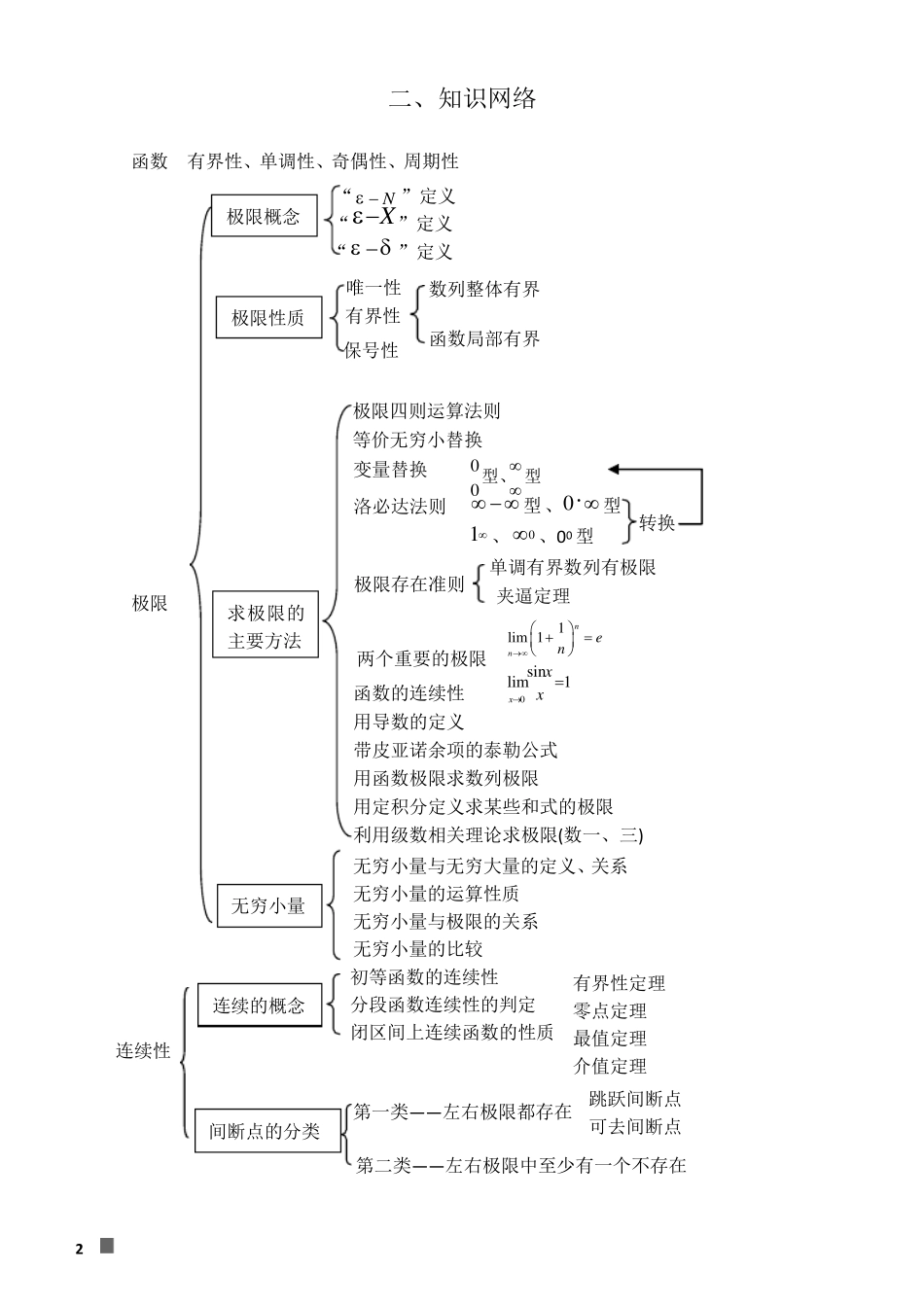
1 第一篇 高等数学 第一章 函数、极限与连续 一、大纲内容与要求【大纲内容】 函数的概念及表示法 函数的有界性、单调性、周期性和奇偶性 复合函数、反函数、分段函数和隐函数 基本初等函数的性质及其图形 初等函数 函数关系的建立 数列极限与函数极限的定义及其性质 函数的左极限与右极限 无穷小量和无穷大量的概念及其关系 无穷小量的性质及无穷小量的比较 极限的四则运算 极限存在的两个准则:单调有界准则和夹逼准则 两个重要极限:0sinlim1xxx,1lim 1exxx.函数连续的概念 函数间断点的类型 初等函数的连续性 闭区间上连续函数的性质. 【大纲要求】 1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系. 2.了解函数的有界性、单调性、周期性和奇偶性. 3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念. 4.掌握基本初等函数的性质及其图形,了解初等函数的概念. 5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左、右极限之间的关系. 6.掌握极限的性质及四则运算法则. 7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法. 8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限. 9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型. 10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质. 2 二、知识网络 极限概念 “N ”定义 “X”定义 “”定义 极限性质 唯一性 有界性 保号性 数列整体有界 函数局部有界 极限存在准则 两个重要的极限 函数的连续性 用导数的定义 带皮亚诺余项的泰勒公式 用函数极限求数列极限 用定积分定义求某些和式的极限 利用级数相关理论求极限(数一、三) 洛必达法则 等价无穷小替换 00型、型 型、0 型 1 、0 、00 型 初等函数的连续性 分段函数连续性的判定 闭区间上连续函数的性质 第一类— — 左右极限都存在 第二类— — 左右极限中至少有一个不存在 跳跃间断点 可去间断点 求极限的主要方法 无穷小量 无穷小量与无穷大量的定义、关系 无穷小量的运算性质 无穷小量与极限的关系 无穷小量的比较 连续的概念 间断点的分类 转换 极限 连续性 函数 有...