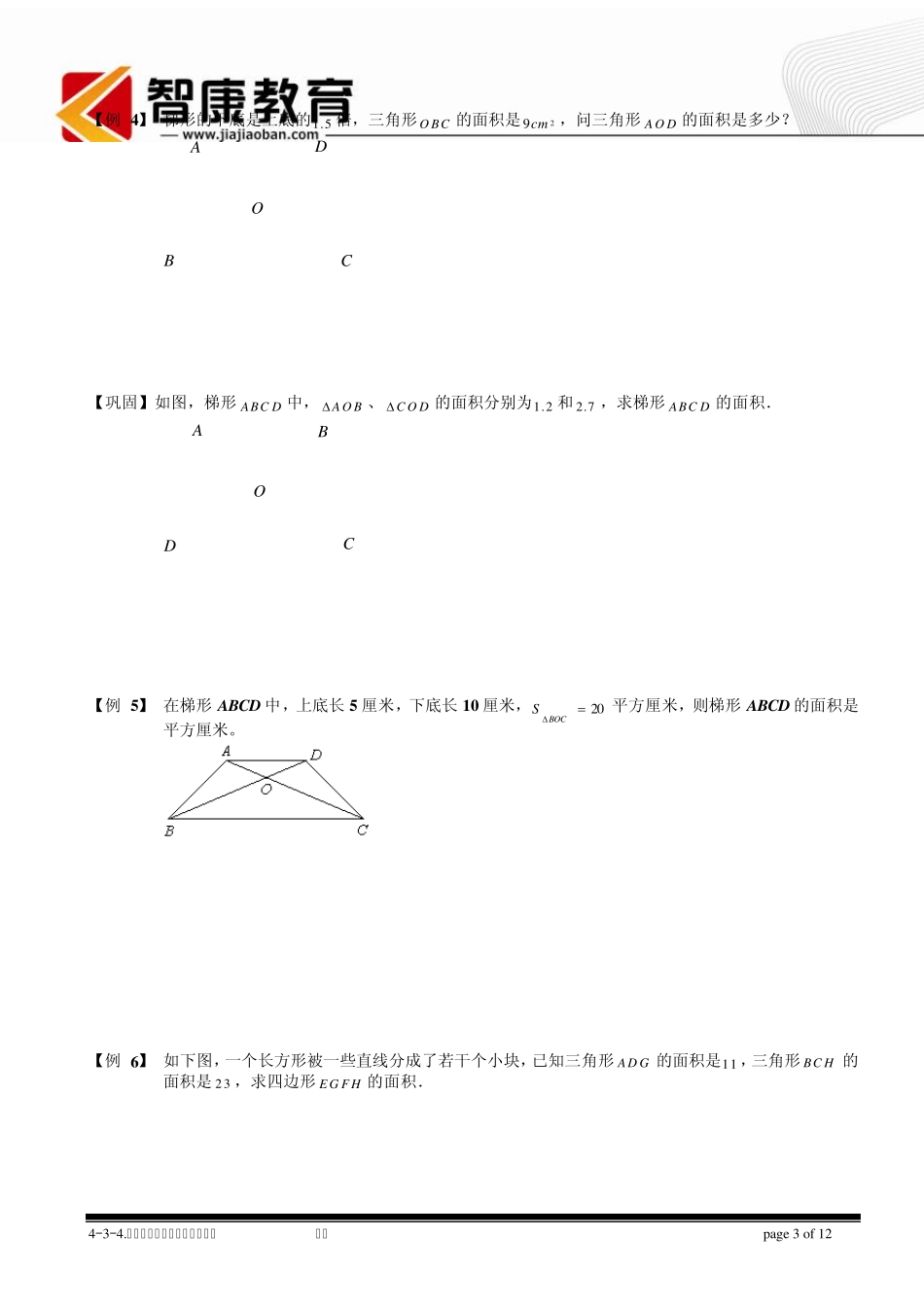
4-3-4.任意四边形、梯形与相似模型 学生 p ag e 1 o f 12 板块二 梯形模型的应用 梯形中比例关系(“梯形蝴蝶定理”): ABCDObaS3S2S1S4 ①2213::SSab ②221324::::::SSSSabab ab; ③ S的对应份数为 2ab. 梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明) 【例 1】 如图,22S ,34S ,求梯形的面积. S4S3S2S1 【巩固】 如下图,梯形ABC D 的 AB 平行于 C D ,对角线 AC , BD 交于 O ,已知AO B△与BO C△的面积分别为 25 平方厘米与 35 平方厘米,那么梯形ABC D 的面积是_ _ _ _ _ _ _ _平方厘米. 3525OABCD 例题精讲 任意四边形、梯形与相似模型 4-3-4.任意四边形、梯形与相似模型 学生 p ag e 2 o f 12 【巩固】 如图所示,在梯形ABCD 中,AB∥CD,对角线 AC,BD 相交于点 O。已知 AB=5,CD=3,且梯形ABCD 的面积为 4,求三角形OAB 的面积。 ABCDO 【例 2】 梯形ABC D 的对角线 AC 与 BD 交于点 O ,已知梯形上底为 2,且三角形ABO 的面积等于三角形B O C 面积的 23,求三角形A O D 与三角形B O C 的面积之比. OABCD 【例 3】 如下图,四边形ABC D 中,对角线 AC 和 BD 交于 O 点,已知1A O ,并且35ABDCBD三 角 形的 面 积三 角 形的 面 积,那么 O C 的长是多少? ABCDO 4-3-4.任意四边形、梯形与相似模型 学生 p ag e 3 o f 12 【例 4 】 梯形的下底是上底的1.5 倍,三角形O BC 的面积是29cm,问三角形A O D 的面积是多少? ABCDO 【巩固】如图,梯形ABC D 中,AO B、C O D的面积分别为1.2 和 2.7 ,求梯形ABC D 的面积. ODCBA 【例 5 】 在梯形ABCD 中,上底长 5 厘米,下底长 1 0 厘米,20BOCS平方厘米,则梯形ABCD 的面积是 平方厘米。 【例 6 】 如下图,一个长方形被一些直线分成了若干个小块,已知三角形AD G 的面积是11 ,三角形BC H 的面积是23 ,求四边形E G F H 的面积. 4-3-4.任意四边形、梯形与相似模型 学生 p ag e 4 o f 12 HGFEDCBAHGFEDCBA 【巩固】如图,长方形中,若三角形 1 的面积与三角形 3 的面积比为 4 比 5,四...