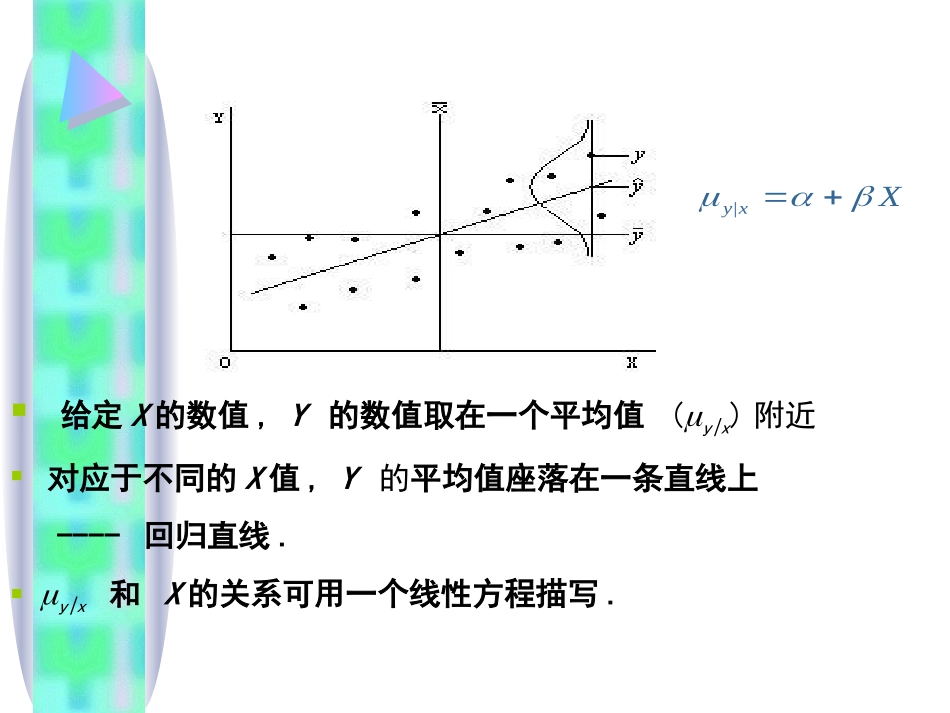
1多重线性回归(multiplelinearregression)2复习:线性相关与回归(linearcorrelationandregression)相关系数r(correlationcoefficient)r的假设检验线性相关线性回归回归方程(regressionequation)其中a为截距(intercept);b为回归系数(coefficientofregression)bXay给定X的数值,Y的数值取在一个平均值(y|x)附近对应于不同的X值,Y的平均值座落在一条直线上----回归直线.y|x和X的关系可用一个线性方程描写.|yxX简单线性回归方程总体样本“Yhat”表示估计值,给定x时y的总体均数的估计值。ˆYabXXXY直线回归方程的求解:最小二乘原理ˆYabXYXˆiiYY线性回归分析的前提条件•线性(linear)–反应变量Y与自变量X呈线性变化趋势•独立(independent)–任意两个观察值相互独立,一个个体的取值不受其他个体的影响•给定X时,Y正态分布(normal)–给定X取值时,Y的取值服从正态分布•等方差(equalvariance)–指对应于不同的X值,Y值的总体变异相同直线回归应用条件LINE示意图[例]携带火柴和发生肺癌间的关系的研究。人们观察发现那些携带火柴的人更有可能发生肺癌。难道这表明携带火柴可能引起肺癌?!这中间存在混杂因素---吸烟客观事实,携带火柴不可能引起肺癌。混杂因素的影响携带火柴?肺癌吸烟混杂因素的定义•当某一危险因素和结果的相关性受第三个变量和危险因素及结果之间关系的影响,这第三个变量称为混杂因素。排除混杂因素的两种方法★分层分析★多元统计分析分层分析的优缺点优点:直观简洁。缺点:当考虑因素较多时分组数量倍增,需要例数较多,有时无法实现。多元统计分析的特点优点有两个:★多元统计分析的资料较容易取得;★多元统计分析可以从整体上分析结果多元统计分析的前提条件★多元统计对所分析资料的分布有一定的要求;★需要有足够大的样本,一般认为,样本的例数n是研究因素个数m的5-10倍。多元统计分析的学习方法•★掌握各种统计学方法的前提条件和应用资料类型。•★借助统计软件(SAS,SPSS,CHISS)完成计算的程序。•★正确解释输出的结果。多重线性回归1.多元统计分析指标的量化法•在作各种多元统计分析时,除定量资料的指标不需要量化外,分类(包括名义性)变量需进行量化,其方法是:(1)二分类•如“性别(SEX)”这个变量,我们不能将其取值“男(或M)”、“女(或F)”直接代入回归方程中去计算,因为它的具体表现不是数据而是文字和符号,而需要用“0”、“1”分别代替两种性别,此时,就说变量SEX是一个二值变量。(2)有序多分类•按照有序的顺序,从低到高(或从小到大)依次赋值:0,1,2,…。•如:家庭月收入情况(元):<50,50-,500-,2000,≥10000分为5个等级,可依次赋值为:0,1,2,3,4。(3)无序多分类•如:若设W代表血型变量,则W的状态就有4种情况,即W=A型、W=B型、W=AB型、W=O型。此时需引入3个哑变量。现假设以O型为基准,则3个哑变量X1、X2、X3可按如下方式来定义:A型——X1=1、X2=0、X3=0;B型——X1=0、X2=1、X3=0;AB型——X1=0、X2=0、X3=1;O型——X1=0、X2=0、X3=0。•一般情况下,若某定性变量有m个水平,就需要引入m-1个二值的哑变量。假如职业分类为工、农、商、学、兵5类,则可定义比分类数少1个,即4个哑变量。编码方法如下:多元相关与线性回归(nultiplepartialcorrelationandlinearregression)•在医学实践中,常会遇到一个应变量与多个自变量数量关系的问题。如医院住院人数不仅与门诊人数有关,而且可能与病床周转次数,床位数等有关;儿童的身高不仅与遗传有关还与生活质量,性别,地区,国别等有关;人的体表面积与体重、身高等有关。人的体重与身高、胸围血压值与年龄、性别、劳动强度、饮食习惯、吸烟状况、家族史糖尿病人的血糖与胰岛素、糖化血红蛋白、血清总胆固醇、甘油三脂射频治疗仪定向治疗脑肿瘤过程中,脑皮质的毁损半径与辐射的温度、与照射的时间例子例子2.多重线性回归(multiplelinearregression)(1)概念:多重线性回归是研究多个自变量与一个因变量之间数量关系并用方程表示出来的一种统计方法。–因变量:近似服从正态...