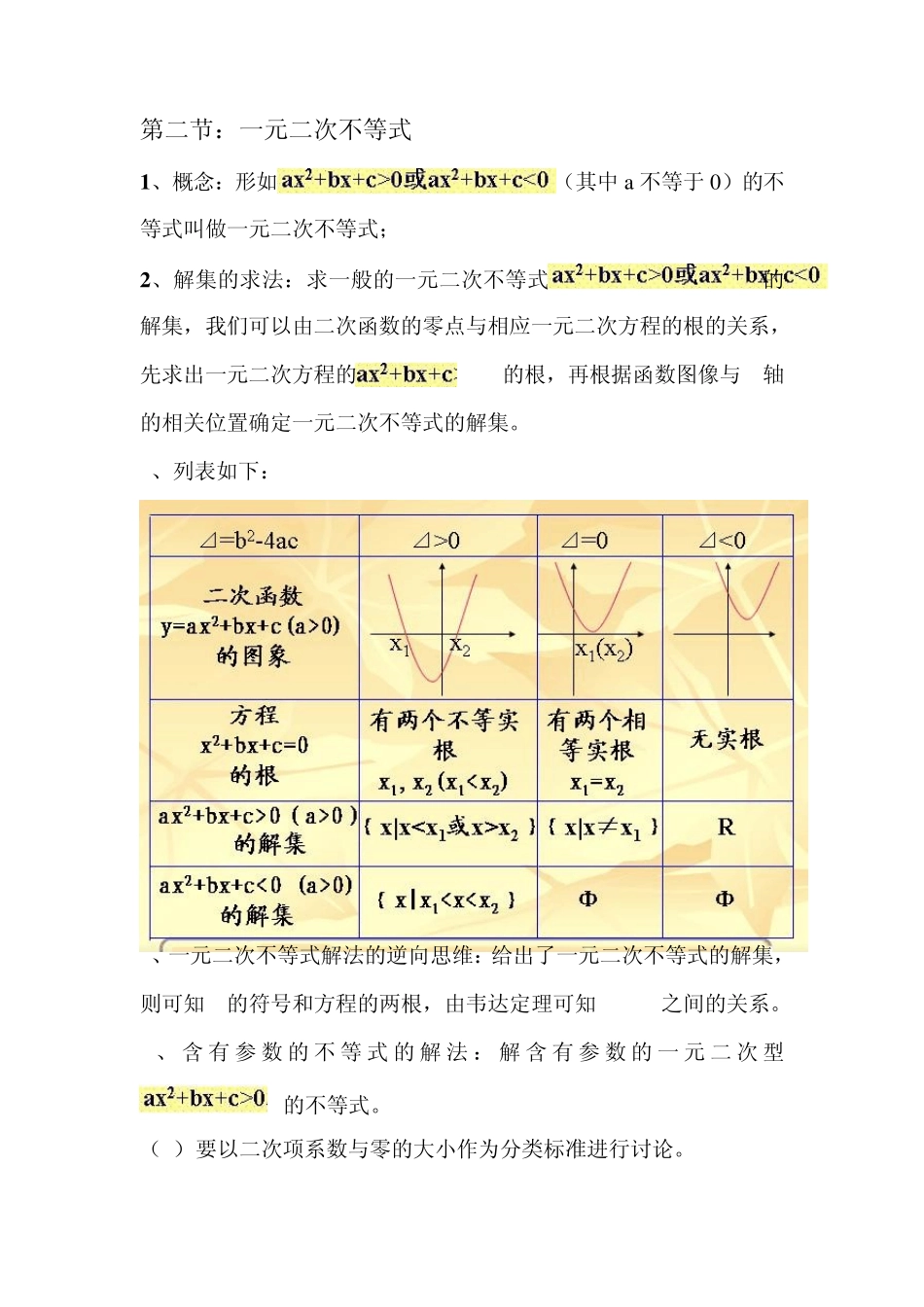
第二节:一元二次不等式 1、概念:形如(其中 a 不等于 0)的不等式叫做一元二次不等式; 2、解集的求法:求一般的一元二次不等式的解集,我们可以由二次函数的零点与相应一元二次方程的根的关系,先求出一元二次方程的= 0的根,再根据函数图像与 x轴的相关位置确定一元二次不等式的解集。 3、列表如下: 3、一元二次不等式解法的逆向思维:给出了一元二次不等式的解集,则可知 a的符号和方程的两根,由韦达定理可知 a,b,c之间的关系。 4、 含 有 参 数 的 不等式的 解 法 :解 含 有 参 数 的 一元二次型的不等式。 (1) 要以二次项系数与零的大小作为分类标准进行讨论。 (2) 转化为标准形式的一元二次不等式(即二次项系数大于零)后,再用判别式与零的大小关系作为分类标准进行讨论 (3) 如果判别式大于零,但两根韩式不能确定,此事再以两根的大小作为分类标准在进行分类讨论; 5、分式不等式的解法:解分式不等式的思想是把分式不等式转化为整式不等式,即:)x(g)x(f>0 转化为 f(x)g(x)>0 )x(g)x(f转化为 f(x)g(x)<0 注意:解此类分时式不等式时,转化为整式不等式后,应注意分子可以取零,但是分母不可以取零。 6、一元高次不等式的解法:数轴穿根法 (1)将 f(x)最高次项的系数化为正数 (2)将 f(x)分解为若干个一次因式的积或二次不可分因式之积。 (3)将每一个一次因式的根标在数轴上,从右上方依次通过每一点画曲线(注意:重根情况,偶次方根穿而不过,奇次方根既穿又过) (4)根据曲线显现出的f(x)值得符号变化规律,写出不等式的解集 (解普通一元二次不等式) 例 1、(1) x2 +3x-10<0; (2)3 x2 +5x-2>0 (跟踪训练)(1)- x2 +4x-5>0 (2)9 x2 -6x+1>0 (3) -3x2 -2x+8≤0 (不等式恒成立问题) 例 2 、(1)3x2 +x-4>0 (2) x2 +2x+3>0 (含有绝对值的不等式) 例 3、(1)x2 -2|x|-3>0 (2) 2x2 +|4x+3|<0 (跟踪训练) (1)︱2x-1︱<3 (2)︱2x2 -x-1︱≥1 (含有参数的不等式) 例4、(1)56 x2 -ax-a2 <0 (2) -x2 +(a-1)x+ a>0 (3)ax2 -(a+1)x+1<0 (分式不等式) 例5、(1)213xx≤-1 xx241>0 (一元高次不等式) 例 6 (1)0322322xxxx (2) (x-2)2(x-3)3(x+1)>0. (跟踪训练) (1)(x-3)(x+1)(x2+4x+4)0. (2)123422xxxx (思考) (x-x2+12)(x+a)<0. (韦达定理与一元二次方程) 例7、已知一元二次不等式ax 2 +bx+1>0的解集为{x︱-1<x<31 },则ab的值为 (一些恒成立问题) 例8、已知不等式x2 +ax+4<0解集为空集,求a的取值范围 (跟踪训练1 )当a为何值时,不等式(a2 -1)x2 -(a-1)x-1<0的解集是全体实数。 (跟踪训练2 )若对 x∈R,ax2 +4x+a≥-2x2 +1恒成立,求实数a的取值范围。