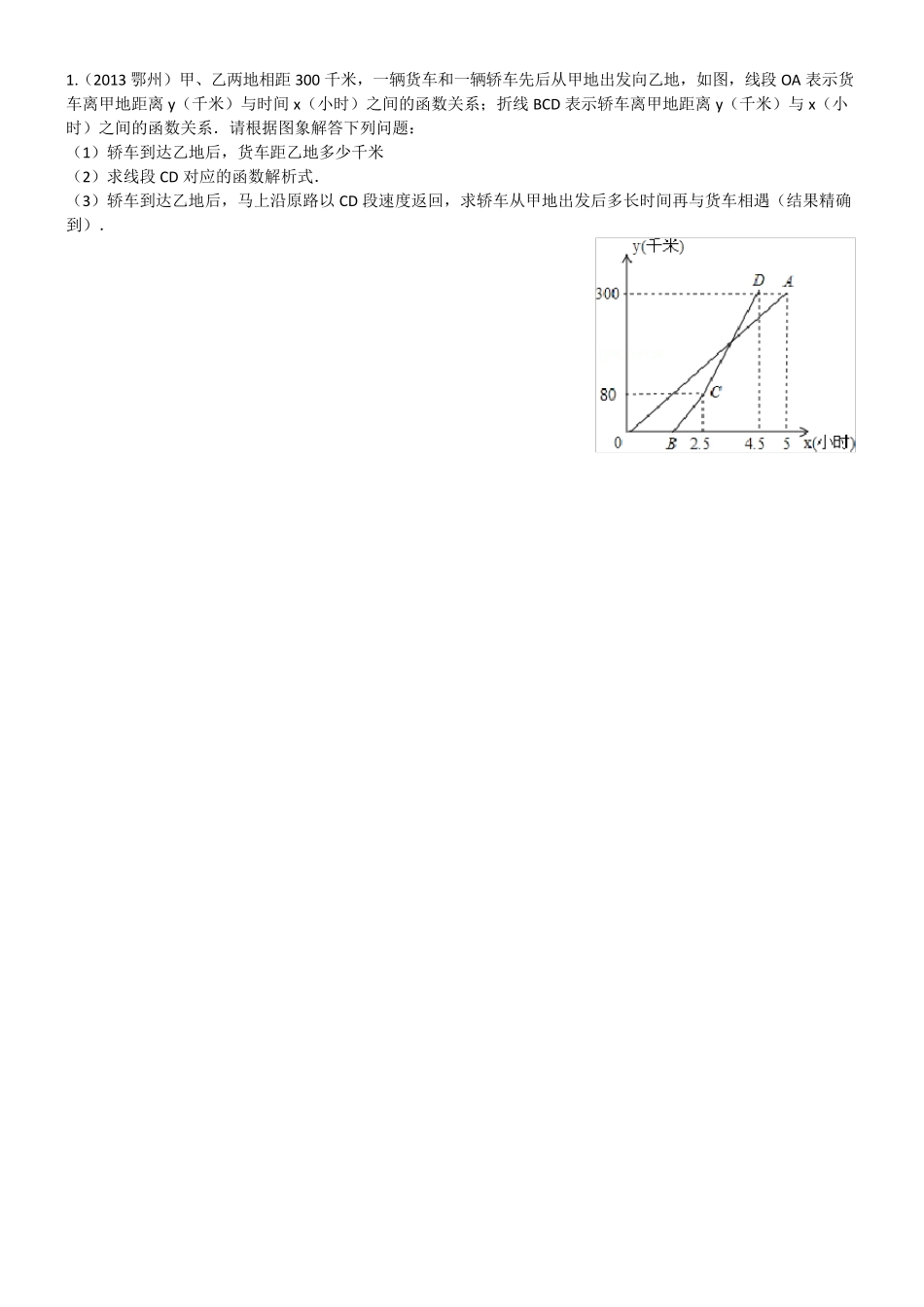
1.(2013 鄂州)甲、乙两地相距 300 千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段 OA 表示货车离甲地距离 y(千米)与时间 x(小时)之间的函数关系;折线 BCD 表示轿车离甲地距离 y(千米)与 x(小时)之间的函数关系.请根据图象解答下列问题: (1)轿车到达乙地后,货车距乙地多少千米 (2)求线段 CD 对应的函数解析式. (3)轿车到达乙地后,马上沿原路以 CD 段速度返回,求轿车从甲地出发后多长时间再与货车相遇(结果精确到). 一次函数的应用 知识点一:一次函数与坐标轴交点和面积问题 1:交点问题 一次函数bkxy的图象是经过(0,b)和(- kb,0)两点。 【典型例题】 1.直线y=-x+2 与x 轴的交点坐标是 ,与y 轴的交点坐标是 2.直线y=-x-1 与x 轴的交点坐标是 ,与y 轴的交点坐标是 3.函数y=x+1 与x 轴交点为( ) A.(0,-1) B.(1,0) C.(0,1) D.(-1,0) 4.直线y=- 32 x+3 与x 轴、y 轴所围成的三角形的面积为( ) A.3 B.6 C.34 D.32 5.直线y=-2x-4 交x 轴、y 轴于点A、B,O 为坐标原点,则 S△AOB= 。 6.若直线y=3x+b 与两坐标轴所围成的三角形的面积是6 个单位,则 b 的值是 。 7.如图所示,已知直线y=kx-2 经过M 点,求此直线与x 轴交点坐标和直线与两坐标轴围成三角形的面积. 2:面积问题 面积:一次函数y=kx+b 与x、y 轴所交的两点与原点组成的三角形的面积为2bk (1):两直线交点坐标必满足两直线解析式,求交点就是联立两直线解析式求方程组的解。 (2):复杂图形“外补内割”即:往外补成规则图形,或分割成规则图形(三角形)。 (3):往往选择坐标轴上的线段作为底,底所对的顶点的坐标确定高。 1. 直线经过(1,2)、(-3,4)两点,求直线与坐标轴围成的图形的面积。 2. 已知一个正比例函数与一个一次函数的图象交于点A(4,3),且 OA=OB (1)求两个函数的解析式;(2)求△AOB 的面积; 3. 已知:mxyl 2:1经过点(-3,-2),它与x 轴,y 轴分别交于点B、A,直线bkxl:2经过点(2,-2),且与y 轴交于点C(0,-3),它与x 轴交于点D (1)求直线21,ll的解析式; (2)若直线1l 与2l 交于点P,求ACDACPSS:的值。 4. 如图,A、B 分别是 x 轴上位于原点左右两侧的点,点P(2,p)在第一象限,直线PA 交y 轴于点C(0,2),直线PB 交y 轴于点D,△AOP 的...